
|
|
 |
|
|
|
|
|
Congruencias Teoría Propuestas Diccionario Herramientas |
Estás en Inicio > Sin decimales > Congruencias > Propuestas
Congruencias
Propuestas
Dentro de estas propuestas encontrarás búsquedas, ejercicios,
demostraciones, ...ordenadas según los siguientes temas:
Contiene ejercicios elementales para comprender las operaciones de congruencias con cuestiones sobre días, semanas, años, olimpiadas, etc.
Para estos ejercicios también puedes usar el modelo de LibreOffice o el de Excel
Usa una hoja de cálculo para estudiar de una forma progresiva las cuestiones que se presentan al dibujar polígonos estrellados. Esta propuesta de trabajo está orientada al Tratamiento de la Diversidad en un Taller de Matemáticas, pues permite ir desarrollando la intuición, generalización y capacidad de encontrar un fórmula de manera progresiva, en la que cada persona llegará a donde pueda, sin presiones.
En el mismo documento se te indica qué hojas de cálculo puedes usar.
La solución para la fórmula buscada es: La parte entera del número que resulta de dividir el indicador de Euler menos 2 entre 2.
![]()
![]()
Extracción de cifras en base B
La dificultad de cada demostración viene dada por el número de "pizarritas":
|
|
|
Fácil |
De tipo medio |
Difícil |
![]() (Adaptación
de un truco de Fernando Blasco en Matemagia) Observa el cuadrado
que hemos destacado en una hoja de calendario
(Adaptación
de un truco de Fernando Blasco en Matemagia) Observa el cuadrado
que hemos destacado en una hoja de calendario
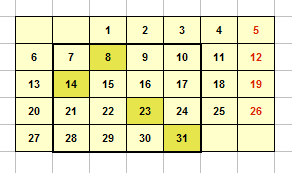
Elige cuatro números de ese cuadrado que estén situados en distintas filas y columnas. Sea cual sea tu elección, la suma de los cuatro será iguala a 76. Busca una justificación de este hecho.
¿Ocurrirá igual en cualquier otro cuadrado (de menos lados) y en cualquier mes?
 Ayuda:
Las semanas forman congruencias módulo 7
Ayuda:
Las semanas forman congruencias módulo 7
Ningún número triangular es congruente con 2 módulo 3
Ayuda: Considera que el producto n(n+1) sólo puede ser congruente con 0 o con 2 respecto al módulo 3
Para todo valor de n se cumple: a) n3- n es múltiplo de 3 b) n5 - n es múltiplo de 5 c) n7 - n es múltiplo de 7
Ayuda: Aplica el teorema de Fermat.
Mediante el Teorema de Fermat calcula el resto de 345 respecto del módulo 23
Ayuda: ¿Qué resto presentará 322? ¿y 344?
Resuelve este sistema
4X + 7Y = 6 (mod 11
X + Y = 6 (mod 11
Ayuda: Por ser el módulo 11 un número primo, no te vas a encontrar con divisores de 0, por lo que puedes seguir el procedimiento de resolución que desees, pero, evidentemente, realizando las operaciones en Z11. Las soluciones son X=1 Y=5
Extracción de cifras en base B
En algunas cuestiones que se pueden resolver con Hoja de Cálculo es imprescindible extraer las cifras de un número en su expresión en una base de numeración dada, generalmente en base 10, de forma que cada cifra esté alojada en una celda distinta, tal como se observa en la imagen

Lo puedes conseguir de la forma indicada en la imagen: En la zona superior de color rosa figuran los números formados al ir extrayendo las cifras, y en la inferior (verde), las cifras extraídas. Son, pues, dos operaciones:
(1) La cifra extraída en cada celda inferior es el resto de dividir el número superior entre la base (su representante en Z/Zb). Se puede conseguir con la función RESIDUO
(2) El número superior se consigue hallando el cociente entero de la diferencia del anterior y la cifra extraída entre la base (función COCIENTE, que existe en OpenOffice.org, pero quizás no en Excel. En este caso se puede sustituir por ENTERO(a/b))
La secuencia podría ser esta (en baso 10): RESIDUO(3245;10)=5; COCIENTE(3245-5;10) = 324; RESIDUO(324;10)=4; COCIENTE(324-4;10) = 32, etc.
El resto de detalles quedan para quien desee construir este extractor de cifras.