
 |
|
|
|
|
|
Estás en Inicio > Sin decimales > Combinatoria > Propuestas > Máquina de combinar

Este material no recibirá actualizaciones frecuentes.
Combinatoria y Probabilidad con Hoja de Cálculo
En este documento puedes consultar el funcionamiento de la hoja de cálculo Combimaq y dos colecciones de problemas (Combinatoria y Probabilidad).
En estas últimas, con Copiar y Pegar, puedes seleccionar los problemas que más te convengan.
Pulsa en estos enlaces para estudiar su funcionamiento
|
|
combimaq2.xlsm |
|
|
combimaq2.ods |
El documento presenta tres apartados distintos:
Hoja de Cálculo "Combimaq"
Pasos para concretar un problema
Abre la hoja de Cálculo "Combimaq", en Excel u OpenOffice
Símbolos
Puedes comenzar por rellenar los símbolos
que intervienen en el problema que deseas resolver.
Escríbelos en la columna
correspondiente.
Combinatoria
Abre la hoja 1 "Máquina de Combinar" y rellena los datos que se te piden arriba
![]()
Número total: El total de objetos
que consideramos. En la figura es un seis.
Pueden ser las seis caras de un dado,
el conjunto M,N,P,O,Q,R, etc.
Número parcial: El número de
objetos en cada arreglo o subconjunto
que formemos.
En este
caso serían 3, por ejemplo 132, 143 541, etc.
Una vez concretados los dos números, total
y parcial, se deben concretar los criterios que seguirán
los arreglos o
subconjuntos.

¿Importa el orden? Si respondemos SI (o activamos su
casilla de verificación)
queremos indicar que
si en un arreglo se altera el orden, se considera otro arreglo distinto
(caso de
Variaciones y Permutaciones) y en caso contrario se considera que es el mismo
arreglo,
es decir, se trata como subconjunto y se trataría de encontrar
Combinaciones.
¿Se pueden repetir símbolos? Esta opción
está clara y permite decidir si permitimos repetir símbolos
en los arreglos (AABC,
ABCC, AAAA,...) o no (ABCD, BACD, ACDB,...)
¿Se fija el numero de apariciones de cada uno?
Este caso sólo es útil para Permutaciones con repetición,
en el que fijamos
el número de veces que aparecerá cada símbolo.
Por ejemplo, las permutaciones de CAMARMA necesitan que se fije que la A se repite tres veces, la M dos, etc.
Dejaremos este caso por ahora.
Una vez concretados los criterios, deberá
aparecer abajo el tipo de arreglos que construiremos
junto con su número total.
Máquina de combinar
Una vez fijados los criterios deberás iniciar el
funcionamiento de la máquina para que produzca todos los resultados.
En la
versión actual llega hasta 500 resultados, pero se pueden ampliar.
| Pulsa sobre el botón "Máquina"
del Cuadro de Controles |
|
|
Probabilidad
En el caso de estudiar la probabilidad deberás rellenar las condiciones para favorables en la Hoja 2 "Probabilidades"
En los ejemplos iremos explicando su forma de uso

Si no te apetece escribir o borrar la "X",
el "SI" o el "NO",
usa la casilla de verificación.
Problemas de Combinatoria (ejemplos resueltos)
Problema ejemplo núm. 1
Queremos hacer una bandera con cuatro franjas de colores
consecutivos distintos.
¿De cuántas formas se pueden
ordenar los colores en la bandera?
Símbolos: Escribe los colores como quieras: verde, azul, rojo, blanco, por ejemplo.
Total: Hay cuatro colores
Parcial: Se toman los cuatro
Repetición: No se repite
Orden: Interviene con toda seguridad, porque es lo que nos interesa.
No arranques la máquina todavía
¿Qué nos piden, variaciones, permutaciones o combinaciones?
Haz un planteo previo, para que sea luego la máquina la que te corrija:
Escribe aquí tu planteo
|
Arranca la máquina de combinar, dale todos los datos y criterios y pulsa el botón Máquina. Resulta una solución de 24 formas de ordenar los colores En la imagen puedes ver el desarrollo completo ¿Ha coincidido con tu planteo? Si no es así, revisa tu planteo y los criterios que le has dado a la máquina. |
 |
Problema ejemplo núm. 2
Los signos 1, X y 2
los escribo como si fuera una quiniela de cinco resultados.
¿Cuántas quinielas
de esas puedo escribir?
Concreta y luego se lo comunicas al ordenador:
Símbolos: 1,X,2
Total: Son 3 símbolos
Parcial: Son quinielas de 5 elementos
Repetición: Se tendrán que repetir. En una quiniela siempre se repiten.
Orden: No es igual escribir un 2 a un partido que a otro.

Obtendrás el resultado de 243. Intenta hacerlo tú:
¿Qué son, permutaciones, variaciones o combinaciones?
¿Se repiten los elementos?
¿Qué fórmula o razonamiento podemos usar?
Escribe aquí tu planteo:
Problema ejemplo núm. 3
¿Cuántas palabras de
seis letras puedo formar con dos fichas que tienen la letra P,
otras tres que
tienen la letra A y una con la letra S?
Símbolos: A,S,P
Total: Son 3
símbolos, pero para que la máquina entienda que son Permutaciones, debes contar
los repetidos.
En total 6:
Parcial: También 6.
Repetición: Se repiten, según la definición.
Orden: Sí influye.
Aquí hay una novedad, y es que hay cuenta de los símbolos: 3 para A, 2 para P y 1 para S
Esto nos obliga a escribir SI en la
pregunta
¿Hay cuenta? y también a rellenar las cuentas a la derecha de los
símbolos.
| Traducción de símbolos | Cuentas | |
| 1 | A | 3 |
| 2 | S | 2 |
| 3 | P | 1 |
Deberá darte abajo el siguiente mensaje:
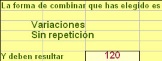
La forma de combinar que has elegido es
Permutaciones Con repetición
Y deben resultar
60
Inicia la máquina y comprueba que resultan 60
palabras.
Si no es así rectifica alguno de los datos.
Problemas de Combinatoria (propuestos)
¿De cuántas formas puedo ordenar las cinco primeras cartas de oros?
Elige los símbolos a tu gusto, por ejemplo: 1o, 2o, 3o, 4o ,5o.
Rellena este cuestionario:
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Inicia la máquina de combinar y observa los resultados. Solución: 120 formasDisponemos de cuatro fichas de colores distintos.
¿Cuántos subconjuntos de dos colores podemos formar?
Símbolos: Pueden ser azul, rojo, verde, blanco, por ejemplo Ayuda:
En los subconjuntos no se tiene en cuenta el orden.
Rellena:
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Inicia la máquina de combinar y observa los resultados.
Solución:
| azul | rojo |
|
| azul | verde |
|
| azul | blanco |
|
| rojo | verde |
|
| rojo | blanco |
|
| verde | blanco |
|
¿Cuántos resultados distintos pueden aparecer?
Símbolos: Los que contiene un dado Rellena:
Número total:
Número parcial:
¿Importa el orden?:
Si se tiran a la vez y caen de cualquier forma, no importará el orden.
¿Se pueden repetir los símbolos? Inicia la máquina de combinar y observa los resultados.
Solución: 56 resultados
¿Y si los tiramos uno detrás de otro y anotamos el orden de aparición?
Solución: 216 resultados
¿De cuántas formas lo puedo hacer?
Símbolos: Elige cuatro frutas, por ejemplo pera, manzana, ciruela y plátano.
Si no te caben los nombres usa abreviaturas: Mz Pr Cr Pl Rellena:
Número total:
Número parcial:
¿Importa el orden?:
Supongamos que lo que te interesa es qué fruta comes, y te es indiferente el orden de comida.
¿Se pueden repetir los símbolos? Solución:
| Mz | Pr |
| Mz | Cr |
| Mz | Pl |
| Pr | Cr |
| Pr | Pl |
| Cr | Pl |
¿Cuántos números resultarán?
Rellena el cuestionario en la Máquina de combinar. Es muy sencillo y debe darte como solución 24 posibilidades.
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
También es fácil. La solución será 120
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
¿De cuántas formas pueden quedar repartidos esos premios?
Rellena los datos y criterios con cuidado.
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Debes obtener esta tabla:
| Ana | María |
| Ana | Juan |
| Ana | Pedro |
| María | Ana |
| María | Juan |
| María | Pedro |
| Juan | Ana |
| Juan | María |
| Juan | Pedro |
| Pedro | Ana |
| Pedro | María |
| Pedro | Juan |
Ayuda: Recuerda que son subconjuntos. ¿Cómo influye esto en el problema?
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Deben resultarte 35 subconjuntos.
No te precipites.
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
| A | A | A | A |
| A | A | A | B |
| A | A | A | C |
| A | A | B | B |
| A | A | B | C |
| A | A | C | C |
| A | B | B | B |
| A | B | B | C |
| A | B | C | C |
| A | C | C | C |
| B | B | B | B |
| B | B | B | C |
| B | B | C | C |
| B | C | C | C |
| C | C | C | C |
¿Cuántos años distintos salen?
Ayuda: Parecen permutaciones, pero hay dos ceros. Se admiten números que comiencen con un cero o dos.
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
| 2 | 0 | 0 | 5 |
| 2 | 0 | 5 | 0 |
| 2 | 5 | 0 | 0 |
| 0 | 2 | 0 | 5 |
| 0 | 2 | 5 | 0 |
| 0 | 0 | 2 | 5 |
| 0 | 0 | 5 | 2 |
| 0 | 5 | 2 | 0 |
| 0 | 5 | 0 | 2 |
| 5 | 2 | 0 | 0 |
| 5 | 0 | 2 | 0 |
| 5 | 0 | 0 | 2 |
¿De cuántas formas pueden elegir la marca?
Ayuda: Si consideraremos el orden, para respetar la identidad de cada amigo o amiga, resultarían 81 formas , pero si sólo nos fijamos en las marcas que se han vendido, sin saber quién las compra, serían 15.
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
Tengo que elegir tres números entre cinco posibles. No puedo repetir y no importa el orden.
¿De cuántas formas puedo elegir? Es muy fácil. Piensa
| 1 | 2 | 3 |
| 1 | 2 | 4 |
| 1 | 2 | 5 |
| 1 | 3 | 4 |
| 1 | 3 | 5 |
| 1 | 4 | 5 |
| 2 | 3 | 4 |
| 2 | 3 | 5 |
| 2 | 4 | 5 |
| 3 | 4 | 5 |
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
Ayuda: Piensa en que sólo nos interesan los géneros, que podríamos representar mediante las letras C, R y E
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución: 60
¿Cuántos billetes distintos han de imprimirse si se distinguen las idas de las vueltas?
Ayuda: Este es muy fácil y directo. Deben resultar 90 clases de billetes.
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
¿De cuántas formas distintas pueden llegar a la meta?
Ayuda: La solución es 120
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
Ayuda: El problema de situar objetos en lugares equivale a formar combinaciones con repetición.
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
¿Cuál es el número total de órdenes en los que han podido aparecer?
Ayuda: La solución es 30. Debes fijar en 5 tanto el número total como el parcial.
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
Se lleva cuenta de los símbolos: 3 de S, 1 de O y 1 de A
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
| S | S | S | O | A |
| S | S | S | A | O |
| S | S | O | S | A |
| S | S | O | A | S |
| S | S | A | S | O |
| S | S | A | O | S |
| S | O | S | S | A |
| S | O | S | A | S |
| S | O | A | S | S |
| S | A | S | S | O |
| S | A | S | O | S |
| S | A | O | S | S |
| O | S | S | S | A |
| O | S | S | A | S |
| O | S | A | S | S |
| O | A | S | S | S |
| A | S | S | S | O |
| A | S | S | O | S |
| A | S | O | S | S |
| A | O | S | S | S |
Dos equipos de fútbol A y B han de
jugar tres partidos sin admitir empates.
(Con prórrogas). ¿De cuántas formas distintas
pueden aparecer las victorias de A y B?
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
Solución:
Problemas de Probabilidad (ejemplos resueltos)
Tiramos un dado 3 veces. ¿Qué probabilidad hay de obtener el seis dos veces?
Abre la hoja combimaq.ods o combimaq.xls y
abre la primera hoja Máquina de Combinar.
Representamos los sucesos por
números del 1 al 6, luego puedes pulsar sobre
el botón números o escribirlos
directamente en la columna de símbolos.
Condiciones combinatorias
Número total: 6 caras
Número parcial: 3 repeticiones
¿Importa el orden?: En los problemas de probabilidad es mejor responder siempre SI
¿Se pueden repetir los símbolos? Sí, porque es el mismo dado el que se tira
tres veces.
¿Se fija el número de apariciones?: No, cada cara se puede repetir entre o y 3
veces.
Condiciones de probabilidad
Pasa a la hoja Probabilidades. Busca la condición Contar las veces que
sale el símbolo y escribe un 6 y 2 veces.
| X | Contar las veces que sale el símbolo | 6 | y que sean | 2 |
Arranca la máquina combinatoria
Te debe dar un resultado de 5/72=0,0694, es decir: 15 casos favorables y 216
posibles.
Razona: ¿Por qué son 216 casos? Puedes usar una celda cualquiera y escribir =6*..... (completa)
Explica este mensaje de la hoja
| La forma de combinar que has elegido es |
|
|
|
|
|
|
| Variaciones |
|
|
| Con repetición |
|
|
|
|
|
|
| Y deben resultar |
|
216 |
¿Por qué los casos favorables son 15? (Es
más difícil: son 15 porque el número
compañero del doble 6
presenta 5 posibilidades y puede estar situado a
izquierda, en medio, o a la derecha... (sigue tú).
Se toma un conjunto de cuatro frutas,
por ejemplo melón, pera, manzana y naranja,
y con ellas se forma una
máquina de juegos con tres frutas. Se pone en funcionamiento.
¿Qué probabilidad hay de obtener tres frutas distintas
en la primera tirada?
Condiciones combinatorias
Número total: Hay cuatro frutas
Número parcial: 3 repeticiones
¿Importa el orden?: En los problemas de probabilidad es mejor responder siempre SI
¿Se pueden repetir los símbolos? Sí, en las máquinas de azar se repiten.
¿Se fija el número de apariciones?: No.
Condiciones de probabilidad
Pasa a la hoja Probabilidades.
Deseamos que no se repita ninguno. Para ello selecciona la condición Que se
repita alguno
(con una X o con la casilla de verificación) y después selecciona
NO
|
|
X | Que se repita alguno |
|
|
|
NO |
Arranca la máquina de combinar y comprueba
que los casos posibles son 64 y los favorables 24,
lo que da un probabilidad de
0,375
Escribe aquí un planteo para justificar esos dos números.
¿Cuántos casos posibles da? _____
¿Cuántos favorables?____
Luego la probabilidad es: ______
Tomamos las cifras 1, 2, 3, 4 y 5 y formamos con ellas
subconjuntos de tres en tres sin repetir
y teniendo en cuenta el
orden. ¿Cuántas posibilidades hay?
¿Qué
probabilidad hay de formar un subconjunto al azar
y que la segunda
cifra sea la suma de las otras dos?
Condiciones combinatorias
Número total: Hay 5 números
Número parcial: 3
¿Importa el orden?: El enunciado afirma que SI
¿Se pueden repetir los símbolos? El enunciado afirma que NO.
¿Se fija el número de apariciones?: No.
Condiciones de probabilidad
Pasa a la hoja Probabilidades.
Este es un caso de condición algebraica. Si has observado el listado de
resultados de la primera hoja
habrás visto la forma de nombrar los elementos de
cada arreglo:SU1, SU2, SU3, SU4,...
Así los escribiremos en la condición de tipo
algebraico.
En nuestro caso la segunda cifra ha de ser igual a la suma de las
otras dos,
luego podemos escribir: SU2=SU1+SU3.
Activa la condición de tipo algebraico y escribe la condición
| X | Condición de tipo algebraico | SU2=SU1+SU3 |
Los casos favorables deberán ser:
| SU1 | SU2 | SU3 | SU4 | SU5 | SU6 | 60 |
| 1 | 3 | 2 |
|
|
|
F |
| 1 | 4 | 3 |
|
|
|
F |
| 1 | 5 | 4 |
|
|
|
F |
| 2 | 3 | 1 |
|
|
|
F |
| 2 | 5 | 3 |
|
|
|
F |
| 3 | 4 | 1 |
|
|
|
F |
| 3 | 5 | 2 |
|
|
|
F |
| 4 | 5 | 1 |
|
|
|
F |
En total resultan 8 ¿Es correcto? ¿Por qué? ¿Falta o sobra algún caso?
¿Cuál sería la fórmula de los casos posibles?
60 =
Si todo ha sido correcto, la probabilidad de este suceso, como habrás leido, es de 8/60 = 0,1333
¿De cuántas formas podemos ordenar las letras AABBC
?
¿Qué probabilidad hay, si elegimos una forma al azar,
de que comience en A y termine también en A?
En este problema hay que llevar cuenta de
las veces que sale cada objeto. Sigue estrictamente estos pasos:
Condiciones combinatorias
Número total: Hay 5 letras, (contando las repeticiones)
Número parcial: Se toman las 5
¿Importa el orden?: El enunciado afirma que SI
¿Se pueden repetir los símbolos? SI
¿Se fija el número de apariciones?: SI, la A 2 veces, la B otras
2, y la C 1.
| Traducción de símbolos | Cuentas | |
| 1 | A | 2 |
| 2 | B | 2 |
| 3 | C | 1 |
Condiciones de probabilidad
Pasa a la hoja Probabilidades.
También es una condición algebraica, pero con alguna novedad:
La A deberemos sustituirla por su número de orden, es decir, 1.
Deberemos multiplicar las dos condiciones
(SU1=1)*(SU5=1),
porque el producto equivale a la conectiva Y y la suma a la O.
| X | Condición de tipo algebraico | (SU1=1)*(SU5=1) |
Te deberán resultar 30 casos posibles (según la fórmula 5!/(2!*2!) ) y
sólo 3 favorables, con una probabilidad de 0,1
Problemas de Probabilidad (propuestos)
Arrojo tres monedas, teniendo
en cuenta su orden.
Encontrar la probabilidad de sacar al menos una cara.
Condiciones combinatorias
Ayuda: El
número de casos posibles debe darte 8
Número total:
Número parcial:
¿Importa el orden?: El enunciado afirma que SI
¿Se pueden repetir los símbolos?
¿Se fija el número de apariciones?:
Condiciones de probabilidad
Debes activar la condición Que aparezca alguno de estos
símbolos
La solución es 7/8
Tengo tres cartas en la mano:
el tres de oros, la sota de oros y el as de copas.
Los ordeno de todas las formas posibles.
¿Cuántos órdenes podré conseguir y qué proporción de esos órdenes comienza con la sota?
Condiciones combinatorias
Número total:
Número parcial:
¿Importa el orden?: El enunciado afirma que SI
¿Se pueden repetir los símbolos?
¿Se fija el número de apariciones?:
Condiciones de probabilidad
Debes activar la condición Cada arreglo debe comenzar
por
La solución es 2/6 = 1/3
En una caja hay 5 bolas numeradas
del 1 al 5.
Hallar la probabilidad de obtener suma 5 si sacamos dos bolas a la vez (no interviene el orden)
Condiciones combinatorias
Número total:
Número parcial:
¿Importa el orden?: El enunciado afirma que NO
¿Se pueden repetir los símbolos?
¿Se fija el número de apariciones?:
Condiciones de probabilidad
Debes activar la condición
Que la suma de símbolos sea
La solución es 2/10 = 1/5
En una Liga Escolar participan
los equipos A B C D E a doble partido.
¿Cuántos partidos habrá en esa Liga?
¿En cuántos de ellos no juega A?
Condiciones combinatorias
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?
¿Se fija el número de apariciones?:
Deben resultarte 20 partidos
Condiciones de probabilidad
Debes activar la condición
Contar las veces que
sale...
La solución es 12/20 = 3/4
Con los símbolos del Morse, punto
y raya.
¿Cuántas palabras de cuatro símbolos puedo formar?
¿Cuántas de ellas tendrán una sola
raya?
Condiciones combinatorias
Número total:
Número parcial:
¿Importa el orden?: En un lenguaje siempre interviene el orden.
¿Se pueden repetir los símbolos?: En el Morse SI
¿Se fija el número de apariciones?:
Condiciones de probabilidad
Debes activar la condición
Contar las veces que sale el
símbolo
Observa el listado que debes obtener
| punto | punto | punto | punto |
|
| punto | punto | punto | raya | F |
| punto | punto | raya | punto | F |
| punto | punto | raya | raya |
|
| punto | raya | punto | punto | F |
| punto | raya | punto | raya |
|
| punto | raya | raya | punto |
|
| punto | raya | raya | raya |
|
| raya | punto | punto | punto | F |
| raya | punto | punto | raya |
|
| raya | punto | raya | punto |
|
| raya | punto | raya | raya |
|
| raya | raya | punto | punto |
|
| raya | raya | punto | raya |
|
| raya | raya | raya | punto |
|
| raya | raya | raya | raya |
|
Ordenamos de todas las formas
posibles las letras "ABCDE", formando nuevas palabras.
¿Cuál es la probabilidad de elegir
al azar una de esas palabras
y que comience por B y termine en vocal?
c:(s1=2)Y((s5=1)o(s5=5))
Condiciones combinatorias
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?: NO
¿Se fija el número de apariciones?:
Condiciones de probabilidad
Esta es difícil y te damos la condición que debes activar.
Recuerda que la
multiplicación equivale a Y y la suma a O, y que las letras se representan por
su número de orden.
| X | Condición de tipo algebraico | (SU1=2)*((SU5=1)+(SU5=5)) |
La solución debe ser 12/120 = 1/10
Se tiran cuatro monedas una detrás
de otra, por orden.
¿Cuál es la probabilidad de que la segunda moneda nos dé un
resultado distinto que la tercera?
Condiciones combinatorias
Número total:
Número parcial:
¿Importa el orden?:
¿Se pueden repetir los símbolos?:
¿Se fija el número de apariciones?:
Condiciones de probabilidad
Como en el anterior, debes usar una condición algebraica: (SU2<SU3)+(SU2>SU3)
La solución es 8/16 = 1/2
En una reunión de vecinos hay cinco
hombres A,B,C,D,E y cuatro mujeres F,G,H,I.
Elegimos al azar dos personas. ¿Qué probabilidad hay de que sean
ambos hombres?
(Por brevedad, no considerar el orden de elección)
Condiciones combinatorias
Número total: 10 (pulsa después en el botón Letras)
Número parcial:
¿Importa el orden?: NO (puedes probar después a responder SI y te dará la
misma probabilidad)
¿Se pueden repetir los símbolos?:
¿Se fija el número de apariciones?:
Condiciones de probabilidad
Como es difícil, te ayudamos:
| X | Condición de tipo algebraico | (SU1<6)*(SU2<6) |
La solución es 10/45 = 2/9 si no consideras el orden y 20/90 = 2/9 si lo consideras.
Se escriben todas las palabras
que tienen las mismas letras que la palabra MARCA.
¿Qué probabilidad hay de
formar una palabra que comience por A?
Condiciones combinatorias
Número total: 5
Número parcial: 5
¿Importa el orden?: SI
¿Se pueden repetir los símbolos?: SI
¿Se fija el número de apariciones?: Escribe bien las cuentas de cada
símbolo
Condiciones de probabilidad
Esta condición es sencilla. Busca en la hoja Probabilidades.
Solución: (Escribimos los favorables) 24/60 = 2/5
| A | M | A | R | C |
|
F |
| A | M | A | C | R |
|
F |
| A | M | R | A | C |
|
F |
| A | M | R | C | A |
|
F |
| A | M | C | A | R |
|
F |
| A | M | C | R | A |
|
F |
| A | A | M | R | C |
|
F |
| A | A | M | C | R |
|
F |
| A | A | R | M | C |
|
F |
| A | A | R | C | M |
|
F |
| A | A | C | M | R |
|
F |
| A | A | C | R | M |
|
F |
| A | R | M | A | C |
|
F |
| A | R | M | C | A |
|
F |
| A | R | A | M | C |
|
F |
| A | R | A | C | M |
|
F |
| A | R | C | M | A |
|
F |
| A | R | C | A | M |
|
F |
| A | C | M | A | R |
|
F |
| A | C | M | R | A |
|
F |
| A | C | A | M | R |
|
F |
| A | C | A | R | M |
|
F |
| A | C | R | M | A |
|
F |
| A | C | R | A | M |
|
F |
Sitúo en fila, y a
ciegas, unas fichas con los números 1,2,3,4 y 5.
¿Qué probabilidad hay de que caigan en orden decreciente?
Condiciones combinatorias
Número total:
Número parcial:
¿Importa el orden?: SI
¿Se pueden repetir los símbolos?: NO
¿Se fija el número de apariciones?:
Condiciones de probabilidad
Usa la condición
Que los símbolos conserven el
orden, porque aunque no sea ese mismo
caso,
tiene la misma probabilidad.
Solución: Es evidente, 1/120