Combinatoria Teoría Propuestas Herramientas
Estás en Inicio > Sin decimales > Combinatoria > Diccionario
![]() Descarga
en PDF (No funcionarán los enlaces externos)
Descarga
en PDF (No funcionarán los enlaces externos)
Pequeño diccionario de Combinatoria
Selecciona una letra o un tema:
A
Una aplicación es una correspondencia en la que cada elemento del primer conjunto le corresponde un elemento del segundo conjunto y solo uno
Triángulo aritmético
Nombre dado también al triángulo de Pascal o Tartaglia.
Llamaremos arreglo en un conjunto finito a cualquier sucesión también finita formada por elementos de ese conjunto. Al ser el arreglo una sucesión, intervendrá en él el orden, y se podrán repetir elementos.
B
Número binomial
Sinónimo de número combinatorio.
C
Es una parte de una permutación que aplica un subconjunto en sí mismo. Por ejemplo
(3 4 5 6)
(5 3 6 4) s(3)=5 s(5)=6 s(6)=4 s(4)=3
(regresa al primero, el 3)
Una permutación es circular o cíclica si es ella misma un ciclo, o que se puede descomponer en un solo ciclo.
Clase de una permutación
Una de las distintas formas de elegir subconjuntos de n elementos dentro de otro conjunto de m elementos. Es claro que cada elección se distingue de otras por los elementos elegidos, no por el orden en el que son elegidos.
Parte de las Matemáticas que estudia las formas de ordenar o elegir elementos en los conjuntos. Se considera fundada por Santiago Bernoulli en su tratado Ars Conjectandi en 1713.
Número combinatorio
Es el número de combinaciones posibles de n elementos en un conjunto de m elementos.
Contar ordenadamente
En Combinatoria es esencial el saber contar ordenadamente los elementos de un conjunto o un arreglo. Para ello se suele usar
Una correspondencia entre dos conjuntos es cualquier subconjunto de su producto cartesiano. En la práctica consiste en asignar una pareja o varias a todos o algunos elementos del conjunto.
CH
D
Llamaremos desarreglo a una permutación de un conjunto en sí mismo en el que no coincide ningún origen con su imagen (no hay puntos fijos). El número de desarreglos posibles en un conjunto de n elementos viene dado por la expresión
Descomposición de un número en sumas
Ver Partición
E
F
Diagrama de Ferrers
Es un diagrama en el que se adosan símbolos formando tantas filas como sumandos entran en la partición, y columnas, siendo la longitud de cada una el valor del sumando. Así, la partición 8=4+2+1+1 se puede representar así:
* * * *
* *
*
*
G
Función generatriz
La función generatriz de arreglos, sucesiones o particiones es una función polinómica cuyos coeficientes coinciden con valores numéricos obtenidos en ellas, especialmente el número total de casos posibles.
Grado u orden de un ciclo en una permutación o sustitución
Es el número de veces que hay que aplicarlo sobre un conjunto para que el resultado sea la identidad. Se puede expresar como potencia: Sg = I , donde S es el ciclo, g su grado e I la identidad.
Grado de una sustitución
Vale la misma definición anterior: Sg = I
, donde S es el ciclo, g su grado e I la identidad.
Si S está descompuesta en ciclos, su grado será el m.c.m.
de los grados de esos ciclos.
Grupo de permutaciones (o sustituciones)
Todas las sustituciones que operan sobre un conjunto forman un grupo para la operación S*T, que consiste en aplicar sobre ese conjunto, de forma sucesiva, las dos sustituciones S y T. Su elemento neutro es la Identidad I. Se le llama grupo simétrico y se representa por Sn, siendo n el cardinal del conjunto.
H
I
Permutación impar
Una permutación es impar cuando posee un número impar de inversiones (o transposiciones). El número total de permutaciones impares de orden n es n!/2
Inversión
Inversión de una permutación
Diremos que dos elementos a y b de una permutación presentan una inversión si están ordenados de forma inversa al orden principal prefijado. Por ejemplo, los números 5 y 2 presentan una inversión en 15342 respecto al orden natural de los números.
Si el número de inversiones de una permutación es par, dicha permutación también se llama par, e igualmente si es impar.
Así la permutación del ejemplo 15342 presenta las inversiones 53, 54, 52, 32 y 42, luego es impar.
L
Los números de Lah sin signo cuentan el número de formas en que un conjunto de n elementos puede dividirse en k subconjuntos ordenados.
Un caso particular, los de segundo índice igual a 2, representa el número de aplicaciones sobreyectivas que se pueden construir entre un conjunto de n elementos y otro de n-1.
M
Coeficiente n1, n2,...
nk, multinomial de índice superior n e
inferiores a, b,... h, con k>2 es una forma de
expresar el número de permutaciones de n elementos con
elementos repetidos en grupos de a, b,... h
elementos. Su valor equivale a
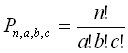
N
Sinónimo de Arreglo o de Selección ordenada
Número
Número combinatorio: Ver Combinatorio
Número de Bell: Se llama número de Bell de un conjunto finito de n elementos, y se representa por Bn al número de particiones distintas que se pueden definir en ese conjunto.
Número de Stirling:
Existen dos sucesiones distintas de números de Stirling, que son
Números de Stirling de primera clase.
Dado el grupo de permutaciones Sn sobre un conjunto de n elementos, llamaremos Número de Stirling de primera clase, S1(n,k), al número de permutaciones de Sn que se pueden descomponer exactamente en k ciclos.
Números de Stirling de segunda clase.
Dado un conjunto de n elementos, llamaremos número de Stirling de segunda clase S2(n,k) al número de particiones distintas de k conjuntos que se pueden definir en ese conjunto de n elementos.
O
El orden en Combinatoria: El orden es un elemento de definición en las combinaciones y permutaciones.
Orden de un ciclo o de una permutación: Sinónimo de grado
P
Permutación par
Una permutación es par cuando posee un número par de inversiones. El número total de permutaciones pares de orden n es n!/2
Paridad de una permutación o una sustitución
Es el carácter par o impar de esa permutación.
Partición de un número natural
Es cada una de las representaciones de ese número como suma de otros naturales no nulos, sin tener en cuenta el orden. Se representa con el símbolo p(n) y se calcula mediante la identidad de Euler
(1-x)-1.(1-x2)-1.(1-x3)-1… = 1+p(1)x+p(2)x2+p(3)x3+…
Triángulo de Pascal
Disposición en triángulo de los números combinatorios o binomiales.
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
1
|
|
|
|
|
|
|
|
|
1
|
|
2
|
|
1
|
|
|
|
|
|
|
1
|
|
3
|
|
3
|
|
1
|
|
|
|
|
1
|
|
4
|
|
6
|
|
4
|
|
1
|
|
|
1
|
|
5
|
|
10
|
|
10
|
|
5
|
|
1
|
Se llama permutación sin repetición a cualquiera de las distintas formas posibles de ordenar un conjunto. El número de permutaciones de un conjunto de n elementos es el factorial de n, n!.
También se define como una aplicación biyectiva del conjunto en sí mismo.
En los distintos órdenes posibles quizás se desee admitir la repetición de algunos elementos un número determinado de veces. Por ejemplo, en la palabra CATAPULTA, si quisiéramos ordenar sus letras, deberíamos admitir que la A se repitiera tres veces y la T dos. Llamaremos permutaciones con repetición a estas ordenaciones.
También se pueden definir estas permutaciones como las formas de distribuir n objetos en k cajas, de forma que cada caja contenga siempre un mismo número determinado de objetos.
Igualmente, coincide con el número de aplicaciones (o funciones) existente entre un conjunto de n elementos y otro de k elementos, en el que el número de antiimágenes de cada elemento está prefijado.
Para calcular el número de permutaciones de este tipo bastará dividir el factorial del número total de símbolos, contando sus repeticiones, entre el número de veces que se repite cada uno.
Este número recibe el nombre de coeficiente multinomial.
Principio de la Adición
Dados los conjuntos A1, A2,...Ak, disjuntos dos a dos, se cumple que
Card(A1È A2È...ÈAk) =Card(A1) + Card(A2) + ... + Card(Ak)
Es decir, que para contar los elementos de la unión de varios conjuntos disjuntos, deberemos sumar.
Principio de la Multiplicación
Si los conjuntos A1, A2,...Ak, son no vacíos, se cumple que
Card(A1´ A2´...´Ak) =Card(A1) ´ Card(A2) ´ ... ´ Card(Ak)
Podemos traducir este principio a la idea de que al combinar mediante pares, ternas, etc. varios conjuntos, el número total de elementos resultantes equivale al producto de los cardinales de los conjuntos que se combinaron.
Principio de Distribución
Este principio se conoce también como Principio de las cajas, del palomar o de Dirichlet
Lo desarrollaremos en dos versiones equivalentes:
(a) Si repartimos m objetos en n cajas, y m>n, entonces, al menos una caja deberá contener 2 objetos o más.
(b) Si se reparten np+m objetos en n cajas, entonces alguna caja deberá contener al menos p+1 objetos.
Principio de Inclusión y exclusión
Se llama así a la fórmula obtenida anteriormente
Card(AÈB) =Card(A) + Card(B) - Card(AÇB)
y a su generalización para más de dos conjuntos. Por ejemplo, para tres sería
Card(AÈBÈC) =Card(A) + Card(B) + Card(C) - Card(AÇB) - Card(AÇC) - Card(BÇC) + Card(AÇBÇC)
En el caso de varios conjuntos aparecerían signos - en las intersecciones de un número par de conjuntos y signo + en las de número impar:
Card(ÈSi) = ∑Card(Si) - ∑Card(SiÇSj) + ∑Card(SiÇSjÇSk) + ... + (-1)n ∑Card(SiÇ...ÇSn)
R
Permutación reducida
Una permutación es reducida si no deja fijo ningún elemento. En su descomposición en ciclos ninguno de ellos tiene orden 1.
S
Sinónimo de Arreglo y de n-pla
Signatura de una permutación
Llamaremos signatura de una permutación al número +1 si es de tipo par o al número –1 si es de tipo impar.
Números de Stirling de primera clase (o primera especie)
Número de Stirling de primera clase S1(n,k) indica, dado el grupo de permutaciones Sn sobre un conjunto de n elementos, cuántas permutaciones se pueden descomponer exactamente en k ciclos.
Números de Stirling de segunda clase (o segunda especie)
Número de Stirling de segunda clase S2(n,k) representa
cuántas particiones distintas de k conjuntos se pueden definir en
un conjunto de n elementos.
Subfactorial de un número natural
Llamaremos subfactorial de n al número de desarreglos de un conjunto de n elementos.
Una sustitución aplicada a un conjunto es cualquier correspondencia biyectiva definida entre los elementos de dicho conjunto. Su número total es el factorial del cardinal de ese conjunto. Es sinónimo de permutación.
T
Se llama transposición en el grupo de permutaciones de un conjunto, a todo ciclo de orden 2. Todas las permutaciones se pueden descomponer en transposiciones, pero no de forma única, aunque se conserva la paridad.
U
V
Una de las distintas formas de elegir subconjuntos de otro conjunto, de forma que cada elección se distinga de otras por los elementos o bien por el orden en el que son elegidos.
W