
 |
|
|
|
|
|
Estás en Inicio > Sin decimales > Divisibilidad > Rutas de los números primos
Rutas de los números primos
Contenidos
Rutas triangulares 1 (hipotenusas incrementadas en una unidad)
Rutas triangulares
2 (hipotenusas incrementadas en dos
unidades)
En esta sección se incluyen esquemas similares a la espiral de Ulam, en el sentido de situar a los números primos en esquemas geométricos, tales como rectángulos, triángulos, espirales, etc, para estudiar las rutas que siguen esos números primos (o también los cuadrados, triangulares, etc.). Con ello se pretenden descubrir propiedades nuevas o bien repasar mejor las ya conocidas.
Cada ruta se estudiará mediante una hoja de cálculo y un documento que contendrá las consideraciones o prácticas propuestas.
Se invita a los lectores de la página a descubrir nuevos hechos en cada una de las rutas.
Se usa una hoja de cálculo para representar los números naturales en filas y columnas, pudiendo destacar en ellas algunos tipos de números, aunque los que nos interesan en este documento son los primos.
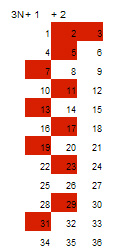
La ventaja de este esquema en rectángulo radica en que aparecen en columna números congruentes, que siguen una misma fórmula lineal del tipo 6N+1, 4N-1, etc.
![]()
Consulta el documento: rectangular.htm
![]()
Usa la hoja de cálculo
|
|
rutrectang.xls
|
|
|
rutretang.ods
|
Se incluyen algunas consideraciones del autor sobre la espiral de Ulam, en las que pone el acento más en las diagonales que no contienen números primos que en las que los contienen. Para ello estudia las formas cuadráticas asociadas, y en especial las del tipo (N-a)(N+a) y N(N+1)-a(a+1)
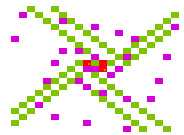
Para el estudio de estas cuestiones se usa una hoja de cálculo que permite representar la espiral de Ulam de forma que se destaquen en ella los tipos de números que deseemos: primos, cuadrados, ...
![]()
Consulta el documento:
![]()
Usa la hoja de cálculo
|
|
ulam.xls
|
|
|
ulam.ods
|
Rutas
triangulares 1 (hipotenusas incrementadas en una unidad)
En estas rutas se distribuyen los números en hipotenusas de triángulos isósceles y rectángulos. Cada hipotenusa contiene un número más que la anterior. Sobre ellas se estudia una conjetura para su demostración por parte de un alumnado avanzado.

Situamos los números naturales siguiendo diagonales, que coinciden con las hipotenusas de triángulos isósceles.
![]()
Se propone una demostración en triangular.htm
![]()
Usa la hoja de cálculo
|
|
ruttriang.xls
|
|
|
ruttriang.ods
|
Rutas triangulares 2 (hipotenusas incrementadas en dos unidades)
Esta disposición triangular usa incrementos de dos en dos en cada línea, de forma similar a los gnomones de la espiral de Ulam. La utilidad de esta disposición es que resalta las formas cuadráticas como líneas rectas, tal como ocurre también en la espiral, con lo que se comprueba que los incrementos impares son los que producen las alineaciones de números primos.
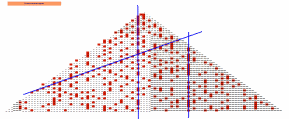
En la imagen se observan las líneas verticales en las que abundan los números primos y aquellas en las que no existe ninguno (formas cuadráticas con descomposición en factores lineales) y también líneas inclinadas que también representan formas cuadráticas. Se ha destacado en la imagen la correspondiente a x2 + x+41, descubierta por Gauss. La limitación de la figura crea la ilusión de que esta diagonal estará formada sólo por primos, cuando falla, por ejemplo, para x=41.
Si se destacan los cuadrados, ocuparán el cateto de la derecha.
![]()
No se ha desarrollado ningún documento
![]()
Usa la hoja de cálculo
|
|
ruttriang2.xls
|
|
|
ruttriang2.ods
|