|
|
Aprender y divertirse con
la Hoja de Cálculo Página personal de Antonio Roldán Martínez |
Inicio Sin decimales Aritmética Divisibilidad Combinatoria Congruencias Juegos Diccionario general Estadística Teoría de Números (R. Parra) |
|
Divisibilidad Teoría Propuestas Diccionario Herramientas Páginas de interés |
||
|
Estás en Inicio > Sin decimales > Divisibilidad > Diccionario |
||
Pequeño diccionario de Divisibilidad
A B C D E F G H I L M N O P R S T U V W
Abundancia
Abundante
Adenda
Aditiva
Algoritmo
Alícuota
Amigos
Antiarmónico
Aquiles
Armónico
Aspirante
Bertrand
Bezout
Brillante
Brun
Casiprimo
Chen
Compuesto
Congruencia
Conjetura
Coprimo
Criterio
Cullen
De la Vallé Pousin
Deficiente
Descomposición
Dirichlet
Distribución de números primos
Divisibilidad
Divisible
Divisor
Factor
Factorización
Fermat
Fórmulas para primos
Fósil
Frobenius
Fuerte
Funciones en Teoría de Números.
Hadamard
Hardy-Littlewood
Harshad
Heterogéneo
Homogéneo
Indicador
Indicatriz
Infinitud de los números primos
Ingham
Intocable
Máximo común divisor
Mersenne
Mínimo común múltiplo
Moran
Múltiplo,
Partes cuadrada y libre
Perfecto
Poderoso
Polidivisible
Polignac
Primario
Primo
Problemas no resueltos
Propio
Pseudoperfecto
Pseudoprimo
Ramaré
Relación
Repunit
Riemann
Ruth-Aaron
Semiperfecto
Semiprimo
Sexy
Sigma
Signatura
Sociable
Sofíe Germain
Submúltiplo
Tau
Thabit idn qurra
Tchebychev
Teorema
Teoría de Números
Triplete
Truncable
A
Dado un número natural N, llamaremos abundancia de N al cociente entre sigma(N) entre N, es decir, entre la suma de sus divisores y él mismo. En los números perfectos la abundancia vale 2, en los deficientes menos de 2 y en los abundantes más de esa cantidad.
Número abundante o excesivo
Un número es abundante si es menor que la suma de todos sus divisores propios, por ejemplo el 12.
Recibe este nombre la función que está definida a partir de una suma extendida a todos los divisores de un número. Los elementos de esta suma se llaman adendum.
Función aditiva en Teoría de Números
Una función g definida sobre números naturales posee la propiedad completamente aditiva si se verifica que g(a*b)=g(a)+g(b) para cualquier par de números natrales a y b.
Si únicamente se cumple para coprimos (primos entre sí), se dirá que es aditiva simplemente.
Un ejemplo de función completamente aditiva es el logaritmo entero o suma de factores primos con repetición. Si se sumaran los factores sin repetirlos, la función sólo sería aditiva.
Es una serie finita de reglas o cálculos en un orden determinado para obtener un resultado a partir de unos datos
Algoritmo de Euclides
Algoritmo que encuentra el MCD de dos números a y b mediante divisiones sucesivas.
Parte alícuota
Una parte alícuota de n es todo divisor propio del mismo, es decir, menor que n.
Sucesión alícuota
Una sucesión alícuota es aquella definida por recurrencia en la que cada término es la parte alícuota del anterior.Su final puede ser cero, un número constante, una sucesión periódica o bien ser desconocida hasta la fecha.
Números amigos
Dos números naturales son amigos si cada uno de ellos es igual a la suma de todos los divisores propios del otro.
Así, son amigos los pares 220 y 284
No hay fórmulas para encontrar todos los números amigos, aunque existen para construir algunos (Ver Thabit idn Qurra)
Número armónico
Los números de Ore también se llaman armónicos.
Número antiarmónico
Es aquel número entero en el que sigma(N) divide a sigma_2(N): la suma de sus divisores divide a la suma de los cuadrados de los mismos.
Número de Aquiles
Es aquel número natural poderoso (todos los exponentes de sus factores primos son mayores que 1) que no se puede expresar como potencia perfecta del tipo m^n con m y n naturales. Por ejemplo 108=33*22
Número aspirante
Es aquel que al iniciar sobre él una sucesión alícuota el final es un número constante. Todos los números perfectos son aspirantes y también algunos no perfectos, como el 25,que produce la secuencia 25, 6, 6, 6, 6...
B
Conjetura de Bertrand
Sea P(x) el número de enteros primos inferiores o iguales a x.
Se cumplirá que P(2x)-P(x)>0 para todo x>1 (o sea, existe un primo entre n y 2n ) (Demostrado por Tchebychev en 1851 y por Erdös de forma más simple)
Teorema de Bézout
Dos números naturales son primos entre sí si y sólo si existen dos enteros m y n tales que m.a+n.b=1
Números brillantes
Son aquellos que son semiprimos y sus dos factores tienen el mismo número de cifras en el sistema decimal. Por ejemplo, 989=23*43
Constante de Brun
La constante de Brun se define como la suma de la serie formada por la suma de los inversos de los números primos gemelos, que el mismo Brun demostró que es convergente.
B= 1/3 + 1/5 + 1/5 + 1/7 + 1/11 + 1/13 + .....
Su valor aproximado es B=1,902160
C
Un número se llama casiprimo de orden K o k-casiprimo cuando su descomposición factorial contiene K factores primos iguales o distintos. Así, los números primos son 1-casiprimos, los semiprimos 2-casiprimos, y así podríamos considerar los 3-casiprimos o 4-casiprimos. El conjunto de todos los números k casiprimos para un k dado se representa con el símbolo Pk. Así, P3={8, 12, 18, 20,...}
Teorema de Chen
Todo número par suficientemente grande es suma de un primo y del producto de dos primos.
Número compuesto
Es el número que no es primo, es decir, que tiene divisores distintos de sí mismo y la unidad.
Congruencia
Relación de congruencia
Diremos que a y b son congruentes módulo n, siendo los tres números naturales, si la diferencia b-a (o bien a-b) es un múltiplo de n. Representaremos la relación de congruencia como a=b (mod n).
La relación de congruencia es reflexiva, simétrica y transitiva, y por tanto da lugar a clases de equivalencia, llamadas también residuales.
Congruencias famosas
Congruencia de Fermat:
Ap-1=1(mod p) si p es primo.
Congruencia de Euler:
Af(n)=1(mod n) donde n no ha de ser necesariamente primo y f(n) es el indicador de Euler de dicho número.
Congruencia de Wilson:
(p-1)!+1=0(mod p) con p primo.
Conjetura
Una conjetura es una afirmación que parece ser cierta en muchos casos, pero que no se ha podido demostrar.
Son conjeturas famosas las de: Bertrand, Fermat, Girard, Goldbach, Hardy - Littlewood, Polignac, Primos gemelos, Waring, etc.
Sinónimo de primos entre sí
Criterio de divisibilidad
Un número natural a divide a otro b si todos los factores primos de a lo son también de b con exponentes iguales o mayores.
Criterios de primalidad
Existen muchos criterios para ver si un número N es primo. Destacaremos:
Clásico: Ir probando posibles divisores entre 2 y la raíz cuadrada N.
Si ninguno es divisor, N es primo.
Fermat: Basado en el pequeño teorema de Fermat, si 2N-1 no es
congruente con 1 módulo N, el número es compuesto. Si es congruente, no se sabrá
si es primo o no.
ARCLP: Test basado en el anterior, pero que es totalmente fiable.
Lucas-Lehmer: Criterio especializado en candidatos a primos que sean
números de Mersenne.
Números de Cullen
Son enteros de la forma n.2n +1
Los primeros números de Cullen son 3, 9, 25, 65, 161, 385, ...
Para todo número primo p distinto de 2 existe una infinidad de naturales n tales que p divide al número de Cullen correspondiente.
El número primo más pequeño de Cullen es 141.2141 +1.
Los siguientes números primos de Cullen son los generados por 4713, 5795, 6611, 18496, 32292,...Existe la conjetura de que haya infinitos números de Cullen que sean primos.
D
De la Vallé Pousin
Ver Hadamard
Número deficiente
Un número se llama deficiente cuando es mayor que la suma de sus divisores propios. Por ejemplo: 21 > 1+3+7
Descomposición en factores primos
Todo número natural se puede descomponer de forma única como producto de factores primos.
Dirichlet
Teorema de Dirichlet
En toda sucesión aritmética a+b.n con a y b primos entre sí existen infinitos números primos.
Por tanto, hay infinitos primos del tipo 4n+1 y también del tipo 4n-1.
Distribución
Distribución de los números primos
Hechos referentes a la distribución de los números primos:
Parte de la Aritmética que estudia los múltiplos y divisores
Relación de divisibilidad
Es la relación que existe entre dos números cuando uno es múltiplo del otro.
Divisible
Sinónimo de Múltiplo
Divisor de un número
Diremos que un número natural a es divisor de b cuando existe otro número natural k que multiplicado por a da por resultado b.
Es aquel que es menor que el número al que divide
Conjunto de divisores de un número
Todo número mayor que 1 tiene al menos dos divisores. El conjunto de todos los divisores posibles de un número natural se obtiene a partir de su descomposición factorial an.bm.cp.dq...mediante técnicas combinatorias y el número total de divisores es (n+1)(m+1)(p+1)(q+1)...
Divisor común a varios números
Es un número que es divisor de todos ellos.
Función divisor
Recibe este nombre y también el de tau, el número de divisores de un número N.
Un divisor d de N se llama unitario si MCD(d,N/d)=1
E
Criba de Eratóstenes
Algoritmo que encuentra la serie de números primos inferiores a uno dado mediante supresiones ordenadas de números compuestos:
Algoritmo de Euclides
Algoritmo para el cálculo del máximo común
divisor de dos números mediante las propiedades del resto de la
división euclídea.
Consulta
en Herramientas un modelo de Hoja de Cálculo que lo contiene.
Teorema de Euclides o de Gauss
Si un número natural n divide a un producto de otros dos a y b y es primo con a, entonces debe ser divisor de b.
Indicador de Euler (o indicatriz, o en inglés Function totient)
Es una función f(n) que indica la cantidad de números inferiores a n y menores que él.
Una fórmula para esta función es
f(n)=n(1-1/p1)(1-1/p2)(1-1/p3)... siendo p1 p2 p3 los factores primos de n
Número extraño
Es aquel que es abundante, pero no perfecto ni pseudoperfecto. El menor número extraño es el 70.
Números extraños
Dos números son extraños o primos entre sí cuando no poseen divisores comunes.
F
Sinónimo de divisor.
Factor primo
Todo número se puede descomponer en producto de factores primos de forma única.
Es la operación de calcular todos o algunos factores de un número. En especial es importante la factorización mediante números primos y la de Fermat. Existen técnicas especiales para factorizar números muy grandes.
Factorización de Fermat
Consiste en representar un número natural como diferencia de cuadrados y después aplicar que a2 – b2 = (a+b)(a-b)
Número de Fermat
| Es aquel que es de la forma |
 |
Fórmulas para generar números primos
La fórmula n2+n+17 produce números primos desde n=1 hasta n=16
2n2+9 produce primos desde n=1 hasta n=8
y n2-n+41, de n=1 a n=40
Dado un número natural N, se multiplican todas sus cifras. Se repite el proceso con el resultado obtenido, hasta obtener un número de una cifra únicamente; a ese número se le llama el fósil de N. Por ejemplo, el fósil de 327 es 8.
Sabemos que dados dos números a y b primos entre sí, existirán dos números enteros x e y tales que se cumpla x*a+y*b=1, y, por tanto, existirán otros dos m y n tales que m*a+n*b=N, siendo N cualquier entero positivo.
La cuestión que planteó Frobenius (problema de las monedas) es para qué números enteros no negativos estos números m y n pueden ser también no negativos, o existirá alguno en el que esto sea imposible. Por ejemplo, 5m+7n nunca es igual a 23 si m y n son mayores o iguales a cero.
Se puede demostrar que para números grandes siempre es posible esta expresión de un número como suma de dos o más múltiplos de otros que sean primos entre sí. Existirá, por tanto, un número que sea el mayor para el que no se cumpla. Este es el llamado número de Frobenius
Número primo fuerte
Si ordenamos y numeramos los números primos, diremos que el primo número n, Pn es fuerte, cuando es mayor que la media aritmética de su primo anterior Pn-1 y su siguiente Pn+1
Funciones importantes en teoría de números
f (n): (Indicador de Euler) Representa cuántos números naturales inferiores a n son primos con él.
s (n): Representa la suma de todos los divisores de n incluido él mismo (es la función sigma de Gauss).
p (n): Representa cuántos números primos hay no superiores a n (también llamada función de números primos
Ω(n): Esta función devuelve el número total de factores primos no necesariamente distintos que figuran e su descomposición factorial. Equivale a la suma de los exponentes con los que figuran los factores primos en dicha descomposición.
ω(n): Representa número total de factores primos distintos que figuran e su descomposición factorial.
G
Teorema de Gauss o de Euclides
Si un número natural n divide a un producto de otros dos a y b y es primo con a, entonces debe ser divisor de b.
Polígonos regulares construibles con regla y compás
Para que un polígono regular pueda dibujarse con regla y compás, ha de tener un número de lados del tipo: n=2r.p1.p2.p3…ps, siendo p1,p2,p3…ps números de Fermat.
Entero de Gauss
Es un número primo del tipo 4n+1, con n natural. Este tipo de números se puede descomponer en una suma de cuadrados enteros.
Primo de Gauss
Es un número primo del tipo 4n+3, con n natural. Este tipo de números no se puede descomponer en una suma de cuadrados enteros.
Números primos gemelos
Dos números primos se llaman gemelos si su diferencia es 2. Por ejemplo, los pares 5 y 7, 17 y 19, 311 y 313,
Se ignora si el número de primos gemelos es infinito, pero se
conjetura que así es.
Erdös demostró que existe una constante c < 1 e infinitos primos p tales que p'
- p < c·ln(p), donde p' denota el número primo que sigue a p.
Chen mostró que existen infinitos números primos p tales que p+2 es un producto
de, a lo más, dos factores primos.
Si dos números son primos gemelos, se demuestra que han de tener la forma 6n-1 y 6n+1 respectivamente.
Se ha demostrado también que dos números n y n+2 son primos gemelos si y sólo si 4((n-1)!+1) = -n (mod (n(n+2))
Números primos gemelos capicúas
Son aquellos que son ambos primos y capicúas y sólo se diferencian en la cifra central, que en uno de ellos es consecutiva de la del otro. Por ejemplo, son gemelos capicúas los pares de números 181 - 191, 373-383, 13831-13931.
Conjetura de Girard
Todo número primo de la forma 4n+1 puede expresarse de forma única como suma de dos cuadrados.
Esta conjetura fue demostrada por Fermat
Conjeturas de Goldbach
Todo número par mayor que 2 es suma de dos primos
Fue propuesta por Goldbach en 1742, en una carta dirigida a Euler. Ha sido comprobada hasta 1014, pero no se ha podido demostrar.
Todo número impar N mayor que 5 es suma de tres primos
Es consecuencia de la anterior.
(Demostrada por Vinogradov (para un número suficientemente grande), tiene como consecuencia que todo número par suficientemente grande es suma de a lo sumo cuatro primos)
Ramaré demostró que todo número par es suma de seis o menos números primos.
H
Teorema de Hadamard
Llamando p (n) al número de primos no superiores a n, se cumple
Lim p (n).ln(n)/n = 1
(Demostrado también por De la Vallé Pousin)
Conjetura de Hardy - Littlewood
Si llamamos p2(x) al número de parejas de primos gemelos menores o iguales que n, se cumple:
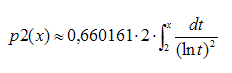
que es una expresión similar a la de la distribución de los números primos.
Un número de Harshad (también conocido como número de Niven), es un número entero divisible entre la suma de sus cifras. Este concepto depende de la base usada. Un número puede ser de Harshad en una base, pero no en otra. Los números de una cifra son todos de Harshad.
Por ejemplo, son números de Harshad 12, 42, 111, 133, 153, etc.
Números heterogéneos
Dos números naturales se llaman heterogéneos cuando no tienen sus divisores primos iguales.
Por ejemplo, son heterogéneos 15 y 20.
Números homogéneos
Dos números naturales se llaman homogéneos cuando tienen los mismos divisores primos, como, por ejemplo, 24 y 36.
I
Indicador de Euler
Ver Euler
Sinónimo del anterior
Infinitud de los números primos
Desde Euclides se sabe que los números primos son infinitos. La demostración de este hecho es una de las más elegantes de la Historia de las Matemáticas.
Teorema de Ingham
Para todo n natural suficientemente grande existe un número primo entre n3 y (n+1)3
Se llaman así a aquellos números que no pueden ser el resultado de la suma de las partes alícuotas de otro número, es decir, de la suma de sus divisores propios.
L
Lagrange
Teorema de Lagrange
Todo número natural es suma de a lo más cuatro números cuadrados.
Llamaremos logaritmo entero de un número natural a la suma de todos sus factores primos, contando sus repeticiones.
Se suele representar por la función sopfr(n). Así, sopfr(28)=2+2+7=11. El valor más pequeño corresponde a sopfr(1)=0 y los máximos coinciden con los números primos, como es evidente.
Se le llama logaritmo porque posee la propiedad
completamente aditiva: sopfr(a*b)=sopfr(a)+sopfr(b). Se cumple por el
hecho de contar las repeticiones de los factores primos. Si se contaran una sola
vez, esta propiedad sólo se verificaría si los números fueran primos entre sí y
daría lugar a otra función que se representa por sopf(n).
M
Máximo común divisor
El máximo común divisor de varios números es el mayor de sus divisores comunes.
Mersenne
Número de Mersenne
Número del tipo 2p-1 con p primo.
Mínimo común múltiplo
El mínimo común múltiplo (MCM) de varios números es el menor de sus múltiplos comunes.
Un número de Hatschard se llama número de Moran cuando el cociente entre él mismo y la suma de sus cifras es un número entero primo.
Múltiplo de un número
Diremos que un número natural a es múltiplo de b cuando existe otro número natural k que multiplicado por b da por resultado a.
Múltiplo común a varios números
Es un número que es múltiplo de todos ellos.
N
Ver Número
Abundante, de Cullen, Deficiente, Extraño,
Feliz, de Fermat, de Harshad, de Mersenne, Narcisista, de Ore, Perfecto,
Ver Números
Amigos, Primos entre sí, Primos Gemelos, Heterogéneos, Homogéneos, Sociables
O
Familia de funciones que cuentan los divisores de un número.
Omega: Cuenta los factores primos de un número sin tener en cuenta las multiplicidades. Así, omega(60)=3
Biomega: Cuenta los factores primos con multiplicidad, como biomega(60)=4
Un número primo recibe el nombre de omipr si su simétrico (el que tiene sus mismas cifras pero invertidas, en base 10) también es primo. Son números omirp 3, 17, 31, 37, 71, 73, 79, 97, 107, 113,...
Un número entero positivo N se llama de Ore o armónico cuando la media armónica de todos sus divisores es un número entero.
P
Todos los números naturales contienen un cuadrado en alguna de sus descomposiciones factoriales (eventualmente valdría 1) y otro factor libre de cuadrados (quizás también 1).
Así, tendríamos, por ejemplo: 80=42*5, 121=112*1, 90=32*10, 15=12*15
Podemos llamar parte cuadrada PC(N) a la primera y parte libre PL(N) a la segunda.
Número perfecto
Diremos que un número es perfecto cuando equivale a la suma de todos sus divisores propios (menores que él).
Los primeros números perfectos son 6, 28, 496 y 8128, ya conocidos en la antigüedad.
Número perfecto por múltiplos
Diremos que un número es perfecto (doblemente, triplemente,…) cuando la suma de sus divisores propios es múltiplo de dicho número. Igualmente, se puede afirmar que la función s (n) es el triple, cuádruple, etc. del número.
Por ejemplo: La suma de los divisores de 120 es
su doble, 240. Lo mismo les ocurre a los números 672 y 523776.
Un número natural es poderoso cuando todos sus factores primos están elevados al menos al cuadrado. Por ejemplo el 72=23*32
Un número natural escrito en sistema decimal es polidivisible si cumple:
Su primera cifra es distinta de cero
El número formado por las dos primeras cifras es múltiplo de 2
El número formado por las tres primeras cifras es múltiplo de 3
El número formado por las cuatro primeras cifras es múltiplo de 4
Y así sucesivamente.
Por ejemplo, 2012, pues 20 es par. 201 múltiplo de 3 y
2012 múltiplo de 4.
Conjetura de Polignac
Para todo número natural k , existen infinitos pares de primos tales que su diferencia es 2k
Fórmula de Polignac
Es una fórmula muy sencilla para encontrar los divisores primos del factorial. de un número natural n. Estos divisores son todos los números primos inferiores a n elevados al exponente r dado por la fórmula
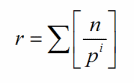
siendo pi las potencias del número.
Número primario
Se llaman números primarios a aquellos que son potencias de primos, como 9, 16, 49 o 169.
Número primo
Un número natural se llama primo si sólo es divisible entre sí mismo y la unidad.
Números primos gemelos
Ver Gemelos
Números primos entre sí
Son aquellos números naturales (no necesariamente primos) que no tienen divisores comunes.
Su MCD es 1. También se les llama extraños, primos relativos o coprimos.
Números primos entre sí dos a dos
Los elementos de un conjunto de números naturales se dicen primos entre sí dos a dos, cuando tomados por parejas, son siempre primos entre sí. Los números 5,15 y 9 son primos entre sí, pero no dos a dos. Sin embargo 4, 9, 25 y 49 sí lo son.
Números primos permutables
Un número primo es permutable cuando todas sus permutaciones de cifras dan lugar a números primos. Por ejemplo el 337.
Problema
Problemas no resueltos en la Teoría de Números
Los siguientes problemas sobre números naturales no han sido resueltos en el momento de redactar esta página:
Número pseudoperfecto
Es un número n es pseudperfecto cuando equivale a la suma de algunos de sus divisores, como 20=10+5+4+1. Si se tomaran todos los divisores se llamaría perfecto.
Número pseudoprimo
Es un número n que cumple que 2 elevado a n es congruente con 2 módulo n Hay infinitos, como 645 o 161038
Pseudoprimo de Perrin
En la sucesión de Perrin, si n es primo, divide a P(n), pero la propiedad contraria no es verdadera: un compuesto puede dividir o no a P(n). La gran mayoría de los compuestos no lo dividen. Los valores de n compuestos que dividan a P(n) son denominados como pseudoprimos de Perrin, como el número 271441.
R
Ramaré
Teorema de Ramaré
Todo número par es suma de 6 o menos números primos.
Relación
Relación de divisibilidad
Diremos que a es divisible entre b cuando b es divisor de a (que por tanto será múltiplo de b)
Esta relación es reflexiva, antisimétrica y transitiva, por lo que constituye un orden. Como no siempre dos números están relacionados por ella, el orden es de tipo parcial.
Relación de congruencia
Dos números están relacionados por una congruencia cuando son congruentes respecto a un módulo dado. Esta relación es reflexiva, simétrica y transitiva y produce, por tanto, clases de equivalencia, llamadas también clases de restos o residuales.
Un número se llama repunit cuando se puede representar como 11111...(N... en el sistema de numeración decimal o en otros. Todo primo distinto de 2 y 5 posee un múltiplo repunit en el sistema decimal.
Los cuadrados de los repunit hasta N=9 unos, se llaman números de Demlo, y la suma de sus cifras es igual al cuadrado de N
Función zeta de Riemann
La función de Riemann sobre un número s viene dada por la serie
x (s) = 1 + 1/2s + 1/3s+ 1/4s + 1/5s …
Se demuestra que coincide con el producto infinito
П1/(1-ps) , donde p recorre todos los números primos.
Un par del tipo Ruth-Aaron está formado por dos números naturales consecutivos que comparten el mismo valor en su logaritmo entero
S
Sinónimo de Pseudoperfecto
Un número natural es semiprimo cuando es producto de dos números primos iguales o distintos. Son semiprimos 4, 6, 9, 10, 14, etc. Se usan en Criptografía con números primos muy grandes.
Números primos sexy son los que forman un par del tipo (p, p + 6), es decir que su diferencia es seis. Por ejemplo, 31 y 37
Con este nombre se conocen todas las funciones que provienen de la suma de los divisores de un número.
Sigma: Llamamos función Sigma a aquella que relaciona cada número con la suma de sus divisores.
Sigma_k: Idéntica a la anterior, suma todos los divisores de un número elevados a la potencia k, por lo que la anterior equivale a sigma_1.
Sigma* (o usigma): Suma sólo los divisores unitarios.
Signatura prima
Es el conjunto de los exponentes que figuran en la factorización de un número en factores primos. Se escriben las repeticiones y se suelen ordenar los exponentes de menor a mayor. Por ejemplo, 60 tiene como signatura {1,1,2}, porque 60=22*3*5
Un conjunto de números se llaman sociables si cada uno de ellos es igual a la suma de los factores propios del anterior hasta llegar de nuevo al primero, es decir, formando una sucesión alícuota cíclica. El periodo de esta sucesión se llama orden del conjunto de números sociables.
Si el periodo es 1, el número es perfecto. Si es 2, es que se trata de números amigos.
Los números sociables más sencillos son 12 496, 14 288,15 472, 14 536 y 14 264
Sofíe Germain
Identidad de Sofíe Germain
x4+4y4= (x2+2y2+2xy)(x2+2y2-2xy)
Teorema de Sofíe Germain
Todo número del tipo a4+4, con a natural y distinto de 1, es compuesto.
Sucesión de Sofíe Germain
Es la formada por los números primos p tales que 2*p+1 también es primo: 2, 3, 5, 11, 23, 29, 41, 53, 83, 89,...
Submúltiplo
Sinónimo de divisor.
T
Recibe el nombre de función tau de un número N al número de sus divisores. También se la denomina función divisor.
Thabit idn qurra
Fórmula de Thabit idn qurra
Permite encontrar pares de números amigos. Se basa en lo siguiente:
Para n>1, si los tres números a = 3.2n-1, b = 3.2n-1-1 y c = 9.22n-1-1 son primos, entonces los números p=2n.a.b y q= 2n.c son amigos
Por ejemplo, para a=11, b=5 y c= 71 resultan 220 y 284.
Los números del tipo 3.2n-1 se llaman números de Thabit y en el sistema de numeración binario vienen representados por las cifras 1, 0 seguidas de la cifra 1 repetida hasta terminar la expresión. Por ejemplo, el número de Thabit 786431 viene representado por 10111111111111111111
Demostró en 1851 la conjetura de Bertrand
Teorema
Ver Teoremas de Bezout, Chen, Dirichlet, Euclides, Gauss, Hadamard, Ingham, Lagrange, Ramaré, Sofie Germain, Vaughan, Vinogradov, Wilson.
Teorema de los números primos
El cociente p(x)/x (ver p(x)) es asintóticamente equivalente al cociente 1/ln(x) para valores de x muy grandes.
Parte de las Matemáticas que estudia las propiedades de los números naturales y enteros. Se considera que la fundó Gauss en sus Disquisitiones aritmeticae (Leipzig 1801) en la parte llamada Teoría de Números Aritmética. Más tarde, Galois fundó la parte algebraica y Minkowski la geométrica.
Triplete de números primos
Es el formado por tres números primos de la forma p, p+2, p+4. Sólo existe el triplete 3, 5, 7, pues otro mayor contendría un múltiplo de 3.
Números primos truncables
Reciben este nombre los números primos que siguen siendo primos aunque se les vayan eliminando las cifras una a una. Unos números permiten esa operación por la izquierda, como 167, que se transforma en 67, también primo, y después en 7. Otros presentan esta propiedad por la derecha, como 599, que pasa a 59 y después a 5. Por último, otros, como el 373, pueden reducirse por ambos lados.
U
Ulam
Espiral de Ulam
Si los números naturales se situan en espiral alrededor del 1, los números primos producen pautas que siguen muy a menudo líneas rectas.
Unicidad
Unicidad de la descomposición en factores primos
La descomposición de un número natural en factores primos es única, lo que constituye el teorema fundamental de la Divisibilidad.
La función usigma asigna a cada número entero positivo la suma de sus divisores propios.
V
Vaughan
Teorema de Vaughan
Todo número par es suma como máximo de 26 números primos.
Vinogradov
Teorema de Vinogradov
Todo número impar N suficientemente grande es suma de tres primos
W
Conjeturas De Waring
Para k=2 y r=4 resulta el teorema de Lagrange: Todo número natural es suma de cuatro números cuadrados.
Hilbert probó que existe g(k) pero no dio un método para calcularlo.
Hardy y Litlewood descubrieron un método que funciona casi siempre.
Wilson
Teorema de Wilson
Para que n divida a (n-1)!+1 es necesario y suficiente que n sea primo.
Por tanto, para p>0 primo tendremos que (p-1)! Es congruente con –1 módulo p
