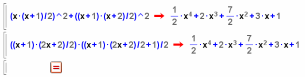Estás en
Inicio >
Sin
decimales
> Propuestas
para el aula y la casa
Propuestas para el aula y la casa

De tipo general
Aritmética y Álgebra
Ideas
para webquest
Búsquedas ordenadas
Ver y calcular
Propuestas para el aula y la casa
En esta sección se
incluirán desarrollos mediante distintos itinerarios de aprendizaje de
propuestas de trabajo destinadas a su uso en las aulas. Se presentarán
en primer lugar en el blog complementario de esta página
Números y hoja de cálculo y
posteriormente se incluirán los desarrollos en esta sección.
En cada propuesta se incluyen
diversos apartados, de los que el profesorado puede elegir los que
desee para adaptarse a las necesidades de sus estudiantes. Se aconseja
la metodología del Taller, que permite fácilmente la atención a la
diversidad del alumnado.
Este material se puede usar y adaptar
libremente para su uso en el aula. Para otro tipo de reproducción o
copia se ruega se cite el autor y la fuente.
De tipo general
Propuestas en ramas
Uso de tablas en el aula
Aritmética y Álgebra
Fechas cruzadas
Cuadrados de bolas
Cuadrados en progresión aritmética
Sistema de numeración binaria
Deconstruir y construir números
enteros
Ideas para webquest
¿En
qué terminan los números triangulares?
Búsquedas ordenadas
Un cuadrado conocido a medias
Compartir o no compartir
¿Cuántas
palabras?
Ver y Calcular
Suma de cuadrados de números triangulares
El fósil de un número
Propuestas en ramas (I)
 Iniciamos la metodología de
"propuestas en ramas" con una colección de propuestas derivadas de un teorema
contenido en el libro “Recreaciones matemáticas 2” de Édouard Lucas:
Iniciamos la metodología de
"propuestas en ramas" con una colección de propuestas derivadas de un teorema
contenido en el libro “Recreaciones matemáticas 2” de Édouard Lucas:
“El número total de
puntos de un juego completo de dominós jamás es igual al cuadrado de un número
entero”
A veces una propuesta sencilla da lugar a
múltiples preguntas. El papel del matemático es el hacerse esas
preguntas, aunque no sepa responderlas. En este caso nos podríamos
plantear: ¿A qué llamamos dominó de n números? ¿Cuál es la fórmula que
nos da el número de fichas? ¿Y el número de puntos? ¿Por qué Lucas
afirma que no son cuadrados perfectos?...
Lo bueno de este planteamiento es que cada
vez que se responde a una cuestión aparecen otras preguntas, con lo que
habremos construido un verdadero árbol con tantas ramas como nuestra
imaginación conciba. En este ejemplo se abrirían múltiples ramas. Los
lectores quedan invitados a recorrerlas y a inventar otras nuevas:
¿Qué es un dominó de número máximo n? (Lo
nombraremos como n-dominó)
Intentar una definición formal,
sin olvidar los “blancos”.
Nuestro
dominó usual se corresponde con n=6 (Un
6-dominó).
Se compone de 28 fichas, con una media de 6
puntos por ficha y un número total de puntos de 168 (demostrarlo)
¿Cuántas
fichas y puntos presenta un n-dominó?
El número de fichas viene dado por la expresión n(n+1)/2 y el de puntos
por n(n+1)(n+2)/2 (demostrarlo).
¿Es cierta la
afirmación de Lucas?
Intenta demostrarla considerando
cómo se reparten los factores primos del cuadrado perfecto entre los
factores n(n+1)(n+2)/2
De una afirmación simple hemos derivado
multitud de cuestiones. Unas sabremos demostrarlas, y otras tendrán que
quedarse en conjeturas, pero su estudio constituirá una verdadera
aventura matemática.
Propuestas en ramas
(II)
En
otra entrada anterior construíamos unas ramas de propuestas a partir de
un teorema contenido en el libro
“Recreaciones matemáticas 2” de Édouard Lucas:
“El número total de
puntos de un juego completo de dominós jamás es igual al cuadrado de un
número entero”
¿Es cierta la
afirmación de Lucas?
Intenta
demostrarla considerando cómo se reparten los factores primos del
cuadrado perfecto entre los factores n(n+1)(n+2)/2
Podemos seguir
planteándonos preguntas sobre este teorema.
Por ejemplo, se podrían considerar proposiciones parecidas y ver en qué
se diferencian del teorema de Lucas:
Esta fórmula es
parecida a la de los números triangulares n(n+1)/2, y sin embargo estos
sí pueden ser cuadrados, como por ejemplo el 36 o el 1225, que son
triangulares y cuadrados a la vez ¿Cuál es la diferencia?
¿Valdría
la afirmación para el producto de tres números consecutivos?¿Nunca
pueden ser un cuadrado perfecto?¿Y la expresión n(n+1)(n+2)/6?
Para quienes no se atrevan
con las demostraciones, una salida es comprobar las afirmaiones con una
hoja de cálculo, cambiando el valor de n
¿Podríamos
conjeturarlos con una hoja de cálculo?¿Cómo?
Por último, nos podemos
dar cuenta de que las expresiones que hemos usado: n(n+1)/2,
n(n+1)(n+2)/2 y n(n+1)(n+2)/6 producen siempre un resultado entero para
n entero a pesar de contener coeficientes fraccionarios
¿Conoces otras con la misma propiedad? Haz un estudio exhaustivo de
este tipo de expresiones enteras.
¿Os apetece crear unas ramas de
propuestas a partir de una cuestión determinada?
En
otro momento publicaremos ramas de propuestas similares. pueden ser
útiles en la Atención a la diversidad, asignando ramas distintas según
los niveles del alumnado.
Uso
de tablas en el aula
Desde la llegada de las calculadoras y los ordenadores el manejo de
tablas se ha ido olvidando en nuestras aulas. Sin embargo, su poder
formativo es muy grande, y son imprescindibles cuando su contenido está
compuesto por datos experimentales, que no se pueden obtener con una
calculadora. ¿Qué capacidades del alumnado podemos enriquecer con ese
uso? Desarrollamos a continuación algunas de ellas:
Consulta
Muchas de las tablas verdaderamente útiles son de doble entrada (en
parte para aprovechar espacio en los libros) pero a los alumnos les
puede suponer una gran dificultad su manejo. Un ejemplo de ello son las
antiguas tablas de cuadrados. En la siguiente imagen reproducimos un
fragmento de una tabla de cuadrados construida con Hoja de Cálculo.
| |
0 |
1 |
2 |
3 |
4 |
5 |
|
2 |
4 |
4,0401 |
4,0804 |
4,1209 |
4,1616 |
4,2025 |
|
2,1 |
4,41 |
4,4521 |
4,4944 |
4,5369 |
4,5796 |
4,6225 |
|
2,2 |
4,84 |
4,8841 |
4,9284 |
4,9729 |
5,0176 |
5,0625 |
|
2,3 |
5,29 |
5,3361 |
5,3824 |
5,4289 |
5,4756 |
5,5225 |
|
2,4 |
5,76 |
5,8081 |
5,8564 |
5,9049 |
5,9536 |
6,0025 |
|
2,5 |
6,25 |
6,3001 |
6,3504 |
6,4009 |
6,4516 |
6,5025 |
|
2,6 |
6,76 |
6,8121 |
6,8644 |
6,9169 |
6,9696 |
7,0225 |
|
2,7 |
7,29 |
7,3441 |
7,3984 |
7,4529 |
7,5076 |
7,5625 |
|
2,8 |
7,84 |
7,8961 |
7,9524 |
8,0089 |
8,0656 |
8,1225 |
|
2,9 |
8,41 |
8,4681 |
8,5264 |
8,5849 |
8,6436 |
8,7025 |
La hemos elegido porque
las cifras que figuran en la fila superior son centésimas, lo que
obliga a realizar un esfuerzo de interpretación. Así, para calcular el
cuadrado de 2,64 se deberá buscar la fila 2,6 y ver dónde se cruza con
la columna del 4, con un resultado de 6,9696
Son muchas las tablas estadísticas y experimentales que pueden
presentar este tipo de dificultades, por lo que creemos que dedicarles
a las tablas algunas sesiones no será tiempo perdido.
Interpolación
Otra utilidad formativa de las tablas proviene de la necesidad de
efectuar interpolaciones debido a que no nos presentan todos los
resultados posibles. Además, en cada interpolación se puede tener una
idea del error cometido, al tener siempre dos valores de la tabla
acotando al verdadero.
Un ejemplo de interpolación directa: ¿Cuál es tu mejor aproximación
para el cuadrado de 2,427 (usando la tabla)?
Buscamos los datos de 2,42 y 2,43, con los resultados siguientes:
Número Cuadrado
2,42 5,8564
2,43 5,9049
Calculamos la tasa de variación: T=(5,9049-5,8564)/(2,43-2,42) = 4,85 y
la multiplicamos por 0,007, que es la cifra siguiente, con un resultado
de 0,03395, que sumado al primer valor nos da una aproximación de
2,4272 = 5,89035 próximo al que nos daría una calculadora: 2,4272 =
5,890329.
No nos extendemos en este tema, pero nuestros lectores pueden ir
reflexionando sobre todas las operaciones mentales que han efectuado
los alumnos para entender y reproducir los cálculos anteriores.
Extensión de la tabla
Interpolación inversa: Encuentra mediante la tabla
el valor aproximado de la raíz cuadrada de 731
En primer lugar deberán entender que esta tabla, mediante
multiplicaciones por potencias de 10, puede resolvernos otros cálculos
que no figuren en ella. En este caso buscamos los dos valores más
aproximados a 7,31, que son
Número Cuadrado
2,7 7,29
2,71 7,3441
Procedemos como en el anterior ejemplo. Calculamos la tasa inversa
TI=(2,71-2,7)/(7,3441-7,29) = 0,18484288 la multiplicamos por
(7,31-7,29), con un resultado de 0,00369686, que sumado a 2,7 nos da
una aproximación a la raíz de 7,31 igual a 2,70369686. Como nos piden
la raíz de 731 y no de 7,31, multiplicamos por 10 (¿por qué?) y
finalmente obtenemos el valor 27,0369686, aproximado al que nos da la
calculadora: 27,0370117
Si revisamos todo lo efectuado, también descubriremos en este cálculo
los conceptos y capacidades que se adquieren con él. No es una
propuesta fácil. Se manejan conceptos de cierta profundidad, por lo que
deberíamos darnos por satisfechos con cualquier logro que se alcance.
Construcción
La construcción de estas tablas estaría reservada al profesorado y a
alumnado de enseñanza media. Una idea, llevada la práctica por el
autor, es la de que los alumnos de Informática construyan tablas con
hojas de cálculo y se las pasen a otros cursos para que practiquen con
ellas. Así el beneficio es doble.
No es trivial esta construcción. Invitamos a los lectores a reproducir
la tabla ejemplo que hemos insertado y podrán comprobar que hay que ir
con cuidado. Proponemos también construir la siguiente tabla de interés
compuesto, en la que dados el tipo de interés anual y los años
transcurridos nos devuelva el tipo acumulado (no el TAE).
| |
Años |
|
|
|
|
|
Tipo |
1 |
2 |
3 |
4 |
5 |
|
1% |
1,00% |
2,00% |
3,00% |
4,10% |
5,10% |
|
2% |
2,00% |
4,00% |
6,10% |
8,20% |
10,40% |
|
3% |
3,00% |
6,10% |
9,30% |
12,60% |
15,90% |
|
4% |
4,00% |
8,20% |
12,50% |
17,00% |
21,70% |
|
5% |
5,00% |
10,30% |
15,80% |
21,60% |
27,60% |
|
6% |
6,00% |
12,40% |
19,10% |
26,20% |
33,80% |
|
7% |
7,00% |
14,50% |
22,50% |
31,10% |
40,30% |
Fechas
cruzadas
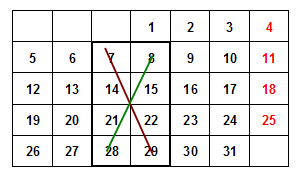
Elige una hoja de calendario, y destaca en
ella un rectángulo cualquiera (ver imagen). Multiplica los números
situados uno arriba a la izquierda (lo nombraremos como F11) y el otro
abajo a la derecha (F22, al final de la línea roja de la imagen,
números 7 y 29). Multiplica también los situados en los vértices
restantes (F12=8 y F21=28 en el ejemplo). Resta los productos y
descubrirás que
El producto de los números de la diagonal
roja F11*F22 es siempre menor que los de la verde, F21*F12,
independientemente del rectángulo que hayas elegido, y su diferencia
(negativa) es siempre un múltiplo de 7
Puedes
trabajar sobre este hecho analizándolo desde varios puntos de vista
(a)
¿Ocurre esto siempre
así? Para demostrarlo puedes llamar X al número más pequeño (7 en el
ejemplo) y a partir de él, le das como nombre una expresión que
contenga X también a los otros cuatro. Desarrolla los productos y te
darás cuenta de que el resultado es siempre negativo.
(b)
Simultáneamente verás
que es múltiplo de 7 (debes demostrarlo o razonarlo bien). Cambia el
salto entre semanas y entre días, y siempre obtendrás ese resultado.
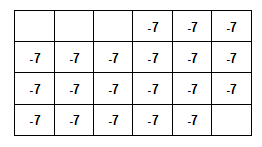
(c)
Observa que en la
imagen, a la derecha de la hoja de calendario, figuran resultados que
son todos -7. Haz tú algo similar usando una hoja de cálculo. Elige un
rectángulo, y en una celda de la derecha escribe la diferencia de
productos que estamos estudiando (en el lenguaje de las hojas de
cálculo. Una fórmula parecida a =B4*C8-C4*B8), y obtendrás un número
negativo y múltiplo de 7. Copia y pega esa fórmula en otras celdas y
siempre obtendrás lo mismo.
(d)
¿Qué ocurriría si
usáramos sumas de diagonales en lugar de productos? Esto es mucho más
fácil…pero debes demostrarlo también.
(e)
Imagina que en un país las semanas fueran de cinco días cada una. ¿Qué
ocurriría entonces con esta cuestión que estamos estudiando?
(g)
Investiga qué ocurre si al usar, en lugar de las diferencias de
productos como =B4*C8-C4*B8 estudiáramos las diferencias de sumas de
cuadrados: =B4^2+C8^2-C4^2-B8^2. Pues resulta que ahora
todas las diferencias son positivas, y siguen siendo múltiplos de 7.
Intenta comprobarlo con la Hoja de Cálculo y después demostrarlo
mediante el álgebra. Llama X a la fecha más pequeña.
(h)
Prueba otros cálculos en diagonal además de productos y sumas de
cuadrados. Investiga por si ves algo interesante.
Cuadrados
de bolas
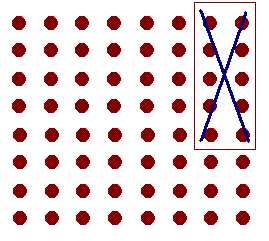
Forma un cuadrado con bolas, situándolas en
filas y columnas, las que quieras. Después elimina 10 bolas e intenta
reorganizar el resto hasta formar otro cuadrado más pequeño, y verás
que resulta imposible, cualquiera que sea el lado del cuadrado que has
formado.
Prueba
entonces a quitar sólo 6 bolas, y observarás que tampoco puedes formar
un cuadrado con las restantes.
Con otros números sí se puede, dependiendo
del lado del cuadrado. Por ejemplo, se pueden quitar 7 bolas a un
cuadrado de lado 4, y 8 bolas a otro de lado 3.
¿Qué tienen de particular el 6 y el 10 para
que ocurra esto?
Descubre más
números con un comportamiento similar, o encuentra una propiedad que
cumplan todos.
También
puedes investigar con una hoja de cálculo, en la que se pueden comparar
todos los cuadrados que desees entre sí, sin que nunca aparezca el 6,
el 10, y otros que no descubrimos.
Cuadrados en progresión aritmética (I)
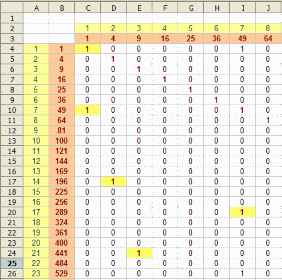
No es difícil encontrar ternas de cuadrados perfectos que estén en
progresión aritmética, tales como 1, 25 y 49, o 4, 100 y 196. ¿Cómo
podríamos encontrar más ternas con una hoja de cálculo? Se podría
organizar una tabla de doble entrada con los cuadrados perfectos, y
después someter a su media aritmética a una condición ¿Cuál?
En la imagen puedes ver el resultado de una búsqueda similar, en la que
se han marcado con un 1 los cuadrados perfectos pertenecientes a una
terna como la propuesta. Si te animas a construir un buscador semejante
podrás encontrar muchas más ternas. Ponte a prueba: ¿Con qué otros dos
cuadrados forma progresión aritmética el número 10404, cuadrado de 102?
Si lo encuentras, nos lo puedes comunicar en forma de comentario.
Para concretar las ternas pedidas hemos recurrido a una exploración
sistemática. Es una forma válida de trabajar en Matemáticas (así se
encuentran los números primos), pero que alguien puede pensar que es
algo perezosa. Podríamos aportar un análisis algo más profundo, pero
eso será en una próxima entrada.
Cuadrados en progresión aritmética (II)
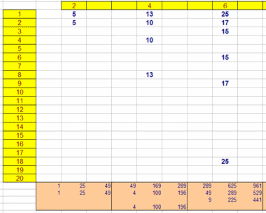
Tal como prometimos, intentaremos un análisis
algo más profundo sobre el tema de encontrar ternas de cuadrados
perfectos que estén en progresión aritmética, tales como 1, 25 y 49, o
4, 100 y 196.

Esto nos da un procedimiento de generación de ternas de cuadrados:
Elegimos cualquier entero p y buscamos un número par h cuyo cuadrado
sea divisible entre p, y mediante la fórmula (1) calculamos n
Ejemplo: p=5, h=10, n=100/10 + 10 + 5 = 25; (n+h)=35: (n-k)=25-10-5*2=5.
Por tanto, los cuadrados en progresión aritmética buscados son: 25, 625
y 1225.
En la imagen inicial
puedes observar una tabla que genera ternas de este tipo de forma
sistemática
Sistema de numeración binaria
Idea para el aula
El
sistema de numeración en base 2 puede tener un aprendizaje totalmente
distinto que el del resto de sistemas en otras bases. Su esencia es la
de intentar formar un número a partir de los sumandos 1, 2, 4, 8, 16,…
tomados sin repetir. Por ello, si se presenta al alumnado un catálogo
de estos números, representados como conjuntos o “montones”, basta ir
eligiéndolos uno a uno para formar el número deseado.
Así,
para formar el número 81, se van sumando los números 64, 32, 16, etc.
añadiendo o quitando cada uno de ellos hasta llegar a la solución 81 =
64 + 16 + 1. La parte más difícil es interpretar después que esta suma
da lugar a la representación binaria 1010001. Para ayudar en ese paso
hemos creado una hoja de cálculo que visualiza tanto la agregación de
los “montones” como la representación binaria a la que dan lugar.
No
se dan aquí indicaciones de cómo usar esta hoja, pues su simplicidad
permite varios itinerarios distintos en el aprendizaje y la elección de
la metodología más adecuada a juicio de cada docente.
Abre
la hoja
binario2.ods
Deconstruir y construir números enteros
Idea para el aula
Tomamos a palabra deconstruir de nuestro admirado cocinero Ferrán
Adriá. Al igual que él descompone un plato en sus constituyentes y lo
vuelve a montar de otra forma, nosotros lo haremos con números. La idea
es descomponer un número entero de alguna forma, usando varias
operaciones, y después volverlo a construir de otra manera totalmente
distinta con los mismos ingredientes.
Lo vemos con el año 2010
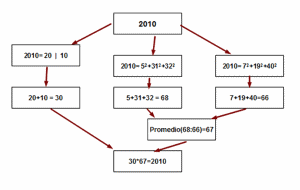
La idea es usar distintas técnicas en cada paso: separar cifras, buscar
factores primos, descomponer en cuadrados, hallar promedios, usar las
cuatro operaciones básicas, etc.
Para un mismo número se pueden establecer competiciones en el aula,
para ver qué esquema de deconstrucción es más elegante, o más complejo,
o con operaciones muy distintas entre sí. Puede ser un entretenimiento
muy formativo, pero se deberá adaptar a la edad de alumnado y a sus
conocimientos.
Ideas para
webquest
¿En
qué terminan los números triangulares?
“Los números triangulares, expresados en base decimal, no pueden
terminar en 2, 4, 7 ó 9”
La metodología de las webquest se adapta muy bien al uso de las hojas
de cálculo y a una buena atención a la diversidad. La afirmación
anterior constituye un punto de partida que admite la organización de
una webquest con distintos itinerarios de aprendizaje según los niveles
del alumnado.
Se puede comenzar con la
frase de arriba, y organizar una webquest para entender bien su
significado y los fundamentos de esa afirmación. Incluimos a
continuación algunos pasos que se podrían seguir:
(a) Definición de número triangular
Se puede buscar en
páginas fiables, tales como Wikipedia
o la misma
Hojamat
(a1) Para el alumnado más aventajado, se sugerirá alguna búsqueda de
carácter histórico sobre estos números.
(a2) Los estudiantes con dificultades pueden copiar imágenes de números
triangulares y pegarlas en un documento.
(b) Fórmula de los
números triangulares
Lo ideal sería que se
pudiera deducir en el aula esta fórmua mediante inducción y discusión
en grupos con la ayuda del profesorado. Así lo ha conseguido el autor
en varias ocasiones, Si no, en las mismas páginas se puede encontrar
dicha fórmula.
Una vez conseguida la fórmula T(n)=n(n+1)/2, se construye una tabla de
números triangulares con una hoja de cálculo.
(b1) Este paso admite una rama de profundización consistente en buscar
en la red propiedades de los números triangulares y experimentarlas con
la misma hoja de cálculo. También se puede intentar generarlos por
recurrencia: T(n+1) = T(n)+n+1
(b2) Una rama de consolidación del aprendizaje consistiría en aplicar
esa fórmula sin el uso del ordenador y reproducir en papel las
operaciones que se han efectuado en la hoja de cálculo.
(c) Terminación de los números triangulares
Ya se está en
condiciones de comprobar que ningún número triangular termina en 2, 4,
7 ó 9, y, lo más importante, intentar justificarlo mediante la fórmula
o razonamiento. Mediante la fórmula T(n)=n(n+1)/2 se puede discutir en
qué cifra puede terminar n, después n+1, su producto y, por último, la
mitad del mismo. Una tabla de hoja de cálculo podría ser muy útil.
(c1) Una actividad de perfeccionamiento consistiría en usar la
propiedad de que “si tomo ocho veces un número triangular y después
sumo 1, resulta un cuadrado”. Se estudian las terminaciones de los
cuadrados impares, se les quita una unidad y se discute su cociente
entre 8.
(c2) Para el alumnado que necesite consolidar lo aprendido, se puede
organizar el cálculo de números triangulares grandes para comprobar sus
terminaciones.
(d) Presentación de resultados
Todo el trabajo
realizado se expone al resto del aula mediante documentos,
presentaciones o puestas en común. Si se dispone de una web de centro,
se incluye en ella todo el material generado en la webquest.
Con estas ideas,
adaptándolas al nivel y características de vuestros estudiantes, podéis
diseñar una o dos sesiones de trabajo que pueden resultar interesantes.
Un
cuadrado conocido a medias
Ideas para el aula
Proponemos una búsqueda ordenada a partir de una cuestión similar a la
siguiente:
Encuentra un
número entero positivo de tres o cuatro cifras sabiendo que su cuadrado
comienza con las cifras 82541…
La idea es resolverlo con calculadora u hoja de cálculo, con lo que la
primera reacción, además de una búsqueda bastante larga, es obtener la
raíz cuadrada de lo que tenemos, y comenzar con las cifras que nos
resulten: raíz(82541)=287.. Pero ¿qué hacemos ahora? ¿irle añadiendo
cifras e ir probando? ¿considerar los decimales?...Puede resultar bien,
y al final de diez intentos conseguiríamos la solución, 2873, pero es
que faltaban dos cifras, y por eso fue fácil. ¿Y si hubieran faltado
tres?
El interés del problema, para un alumnado de Enseñanza Secundaria, es
que al ignorar a priori cuántas cifras faltan, no sólo debe pensar en
la raíz del número dado, sino también en la raíz del número que queda
al eliminar una cifra. Lo vemos con este ejemplo:
¿Qué número
tiene un cuadrado que comienza por 824… sabiendo que faltan por
escribir una, dos o tres cifras?
Probamos el procedimiento anterior: Raíz(824)=28,7
Si faltaran dos cifras, deberíamos probar con números cercanos a 285,
286, 287,…y ninguno de sus cuadrados comienza con 824.
Probamos la hipótesis de que falte una cifra, con lo que deberíamos
basarnos en Raíz(82)=9,05, y obtenemos otro fracaso, pues desde 90 a
100 ningún número produce un cuadrado que comience con 824.
Por último, probamos con tres cifras más. En teoría deberíamos probar
desde 2850 a 2880, por ejemplo, y con paciencia llegaríamos a
2872^2=8248384
Desarrollo
en el aula
¿Qué se podría lograr en el aula con este ejercicio? Destacamos algunos
aprendizajes y estrategias que se podrían descubrir:
Posibles objetivos
Darse cuenta de que la
raíz cuadrada actúa sobre pares de cifras
Descubrir búsquedas
binarias cuando las cosas se ponen difíciles (caso de tres cifras)
Aprovechar los decimales
que nos dan las calculadoras (aquí no lo hemos hecho)
Saber cambiar de
estrategia a tiempo.
Posible desarrollo
Se lee en común la cuestión propuesta por el procedimiento que se
juzgue más adecuado.
No se debe nombrar la raíz cuadrada en un principio, salvo que
transcurran los minutos y no se logre ningún avance. Se plantea la
cuestión, explicando las dudas que surjan y se comienza el trabajo de
búsqueda. Es conveniente tener preparados varios ejemplos más con
distinto número de cifras para intentar conseguir que se resuelvan
varios en una misma sesión.
Al finalizar el trabajo se organiza una puesta en común para compartir
resultados y estrategias. Si el proceso va lento, se puede abrir una
debate breve cuando hayan aparecido dos o tres soluciones.
Agrupamiento del
alumnado
Puede organizarse en grupos de dos o individualmente. Si se ve
necesario para atender a la diversidad, se pueden permitir grupos de
tres.
Material
(1) Calculadora y papel: Tiene la ventaja de que se puede organizar el
trabajo de forma individual, pero las búsquedas pueden ser exasperantes.
(2) Hoja de cálculo: Obliga a organizar equipos, pero se da facilidad
para organizar mejor las búsquedas y aprovechar la posibilidad de
ordenar los intentos en serie en una columna.
Evaluación
Debe obligarse a la escritura de conclusiones, ya sea en otra sesión, o
bien fuera del horario escolar. En este ejercicio es tan importante la
velocidad como el descubrimiento de estrategias y atajos.
La evaluación se realizará atendiendo al documento producido y a las
notas tomadas por el profesorado respecto al desarrollo del trabajo,
número de soluciones, variedad de métodos, etc.
Compartir o no compartir
Propuesta de investigación en el aula
Uno de los teoremas más
elegantes de la Teoría de la Divisibilidad afirma que la probabilidad
de que al escoger al azar dos números naturales, estos resulten primos
entre sí, es decir, que no compartan divisores primos, es igual a
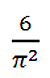
Es evidente que la comprensión y demostración de este teorema sobrepasa
las capacidades del alumnado de Enseñanza Media, pero se puede intentar
una aproximación intuitiva al mismo. Podríamos plantearnos distintas
fases de una experimentación.
Fase 1
Experimentación y
cálculo
Experimentación
con frecuencias y con números acotados
El teorema que presentamos contiene infinitos en su enunciado. Por una
parte, la variable aleatoria usada abarca todos los números naturales.
Por otra, no existe máximo en la muestra que podamos estudiar. Por eso,
en el aula nos podemos restringir a números acotados (por ejemplo, los
menores que 100) y a muestras pequeñas, o bien toda la población de los
mismos, que en este caso equivaldría a 10000 pares de números. Al
alumnado entonces hay que advertirle que estudiaremos frecuencias, no
probabilidades.
Experimentación
Se pueden usar bolas del bingo (por ejemplo, cien) con reposición, e ir
planteando para cada par si tienen divisores comunes o no. Se puede
organizar por grupos o con toda el aula. Cada alumno o alumna copiará
en su cuaderno los pares y si son primos o no, para obtener frecuencias.
Con ello obtendremos, una tabla parecida a la siguiente:
Comparten divisores 79
Son primos entre sí 121
Total
200
Frecuencia relativa 0,6050
Si repetimos el experimento varias veces o acumulamos resultados de
varios grupos, nos acercaremos al verdadero valor de la probabilidad
para números menores que 100, cuyo valor exacto es 6087/10000 = 0,6087
Cálculo
¿Cómo podemos encontrar esa probabilidad exacta con una hoja de
cálculo? Si no deseamos acudir a macros, podemos construir una tabla de
doble entrada, por ejemplo de 100 por 100, y calcular la función de
Excel y Calc =M.C.D(a,b) para cada par.
En la imagen puede ver un fragmento de esa tabla:
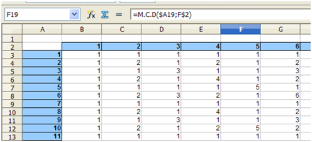
Sobre esta ella aplicamos la función =CONTAR.SI(Rango de los mcd;1),
para contar los valores 1, y nos resultarán 6087 sobre 10000.
Ampliación
Después, como ampliación, se pueden encargar experimentos con cotas más
altas, como 200, o cálculos de la probabilidad exacta para números
pequeños, como del 2 al 20.
Siempre obtendremos frecuencias o probabilidades cercanas al 0,6, con
lo que el alumnado sospechará que el verdadero valor es el 60%, por lo
que en una segunda fase habrá que sacarle del error:”Esto no es tan
simple”.
Un punto delicado es el de saltar a la idea de infinito, pero en estos
niveles siempre haremos lo que podamos, sin forzar.
Fase 2
Simulación
Con una hoja de cálculo se pueden simular dos columnas de números
aleatorios. La fórmula, como puede ser complicada, se debe sugerir.
Recomendamos usar =ENTERO(1+ALEATORIO()*COTA) , siendo COTA la que
deseemos marcar para los números del experimento, porque funciona bien
en Excel y Calc y no da problemas al recalcular.
En una nueva columna escribimos su M.C.D y contaremos, con CONTAR.SI,
la cantidad de valores 1 que aparezcan. Dividimos después por el número
de filas usadas y tendremos una aproximación a la probabilidad.
Esta tabla contiene el final de una simulación de números con cota 2000
en una simulación de 2000 filas:

El total de pares se ha calculado con la función CONTAR, el de coprimos
con CONTAR.SI aplicado al valor 1, y la frecuencia mediante división.
Si deseas una simulación más potente mediante macros, puedes usar este
código:
Sub compartir
Dim i,n,cota,m
dim a,b
randomize
cota=val(inputbox("Cota"))
n=val(inputbox("Número de repeticiones"))
m=0
for i=1 to n
a=int(rnd()*cota+1)
b=int(rnd()*cota+1)
if mcd(a,b)=1 then m=m+1
next i
msgbox(m)
End Sub
Con esta macro podemos preparar tablas en las que se observe su
acercamiento al límite teórico. La siguiente tabla está construida con
10000 simulaciones para cada nivel:
N
100
500 1000 10000 100000 1000000
P 0,6098 0,6081 0,6119 0,6060 0,6094 0,6093
Se observa la gran estabilidad de este cálculo, ya que a veces los
errores propios de la simulación esconden la convergencia al límite.
Límite similar
También es igual el límite de la frecuencia con la que aparecen los
números libres de cuadrados. Se llaman así a aquellos que no son
divisibles entre ningún cuadrado, como 21 o 30. Es un poco complicado
buscar esos números de forma manual, por lo que podemos usar una
función nueva en la hoja de cálculo, cuyo código puede ser:
Public function
librecuad(a)
dim m,n,p
dim divi as boolean
if a<4 then
librecuad=1
else
divi=false:n=2:p=1
while divi=false and n<=int(sqr(a))
if a/n/n = int(a/n/n) then divi=true:p=0
n=n+1
wend
librecuad=p
end if
end function
Es una función que nos devuelve un
1 si el número está libre de cuadrados, y 0 si contiene alguno.
Se pueden crear columnas paralelas como las de la imagen
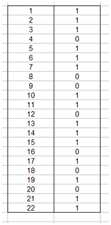
y después usar la función CONTAR para calcular la frecuencia
Si diseñamos dobles columnas para números de mil en mil, nos
sorprenderemos de la estabilidad de las frecuencias y su cercanía al
límite
¿Cuántas palabras?
El otro día, después de jugar con mi nieta a inventar palabras, se me
ocurrió una experiencia para el aula, y es la de organizar un proyecto
de estimación del número de palabras que se pueden construir en nuestro
idioma. ¿Cuántas pueden ser? ¿veinte millones? ¿sólo unos miles? ¿miles
de millones? ¿trillones?... Quizás así, de improviso, no se te ocurra
ninguna idea.
Parece ser que reuniendo todas las variantes locales, no llegaríamos a
unos pocos cientos de miles de palabras usadas realmente (los
diccionarios no suelen traer más de 90.000), pero aquí nos interesan
las posibles palabras que podríamos inventar.
Objetivo
del proyecto:
Estimar el número de
palabras posibles que puede contener nuestro idioma.
Como el planteamiento es muy amplio, se deberían tener en cuenta estos
detalles:
* Se puede acotar la estimación a palabras de no más de cinco sílabas.
Si no, nos toparíamos con molestos infinitos.
* Es bueno que la estimación no se base sólo en técnicas de conteo.
También se deben repasar los conceptos de sílaba directa, inversa o
mixta, los diptongos y los triptongos.
* Lo normal es que en la puesta en común aparezcan grandes
discrepancias en las estimaciones, lo que dará pie a discusión en grupo
e incluso elección de la mejor estimación.
¿Qué
podemos conseguir con esta experiencia?
* Estudio de las sílabas y palabras como objetos de un conteo
* Repaso de las técnicas de contar
* Asimilación del concepto de estimación y de orden de magnitud.
* Ejercitación en la puesta en común, muy necesaria en un tema que
puede admitir variantes en resultados y métodos.
* Experimentación de concurrencias entre dos materias muy distintas,
como la Gramática y la Combinatoria.
* Construcción de esquemas ordenados.
El proyecto podría tener estas fases:
Recuento de
sílabas
La primera tarea podría
consistir en contar el número posible de sílabas que comienzan con una
letra determinada. No hay que ser muy exigentes en este primer paso,
pero deberán considerar sílabas directas, mixtas e inversas en su caso.
Por ejemplo, para la letra B se deberían considerar al menos estas: BA,
BE, BI, BO, BU, BRA, BRE, BRI…BLA, BLE,…BAR, BER,..BAS, BES,…BAL,…BLAS,
BLES,…BIA, BIAS, BUAI, BONS,…
No se trataría de realizar un estudio exhaustivo (imposible sin
convenios previos), sino de aproximarnos al uso general de nuestro
idioma. Es posible que se olviden sílabas como INS, TRANS, ABS,… pero
no hay que darle importancia. Se trata de una estimación.
Se podrían contar mediante un producto cartesiano:
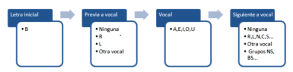
Este esquema nos una idea del número de sílabas que forma la B (sólo
una aproximación)
1*8*5*12 = 40*12 = 480
Insistimos en que esta fase no ha de ser demasiado cuidadosa. Habrá
letras que formen unas 480 sílabas y otras (como la A) que formen
menos. Esto es lo bueno, que todo el planteamiento pueda ser discutido.
El mismo estudio que sugerimos sobre la B se podría repetir con las
demás letras. Por simplificar, supongamos que el número medio de
sílabas por letra fuera de 300 y que letras válidas en español
contáramos 26. Ello nos daría una estimación de 7800 sílabas distintas.
Recuento de palabras
Seguimos con el
producto cartesiano. El número de palabras entre una y cinco sílabas
sería: 7800+78002+78003+78004+78005= 2,88754E+19
¿A que no esperabas que fueran tantas? Son trillones. Ahora te toca
criticar esta estimación, pero reconocerás que no me van a faltar
palabras para inventar con mi nieta.
Pasamos por alto que las sílabas inversas sólo aparecen en primer
lugar. Se trata de dar una idea. Quizás a algún lector le apetezca
realizar un estudio más fino.
Puesta en común
Este paso es
imprescindible. Lo ideal sería efectuarlo con una PDI y libre discusión
entre grupos. Puede durar una hora o más, pero no será tiempo perdido.
No se trata de estimar mejor o peor, sino de llegar a una idea sobre el
orden de magnitud y, lo que es más importante, a un intercambio de
métodos.
Publicación
También este paso es
insoslayable. Repito algo que siempre comento: No has aprendido un
concepto si no sabes comunicarlo a otros. Se podrá efectuar en formato
de documento o presentación, como una memoria de la experiencia o
usando la web o el blog del centro.
Como siempre en este blog, no sugerimos nivel educativo ni momento
idóneo para organizar este proyecto. El profesor jubilado no quiere
opinar sobre ello. Todo eso queda ya un poco lejano.
Ver y Calcular
Suma
de cuadrados de números triangulares
El estudio de cuestiones aritméticas deriva
pronto a cálculos algebraicos, generalmente tediosos, y, en algunos
casos, también a esquemas geométricos. Estos dos caminos, el algebraico
y el visual se complementan perfectamente. Los números figurados, por
su propia definición, son buenos elementos de unión entre ellos. Veamos
un ejemplo cn números triangulares:
“Llamamos T(n) al enésimo numero natural. ¿Qué obtenemos si sumamos los
cuadrados de un número triangular T(n) y de su siguiente T(n+1)?
Orientación algebraica
Conjetura: Diseñamos una tabla de números triangulares en una hoja de
cálculo y en una columna adjunta calculamos la suma de cuadrados pedida
para todos los casos posibles. Fácilmente se descubre una ley de
formación. No indicamos el resultado, tan sólo que es un número
triangular. ¿Cuál?
Cálculo: Mediante cálculos algebraicos se puede verificar la conjetura.
Basta desarrollar la expresión y comprobar su resultado con el
imaginado. En la imagen tienes un desarrollo efectuado con la
calculadora Wiris. La conjetura está un poco escondida.
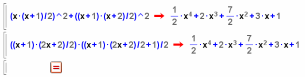
Orientación geométrica
Podemos atrevernos a pensar que si T(n) es un número triangular, su
cuadrado se podrá representar por otro número triangular idéntico a él,
pero sus elementos no serán puntos o bolitas, sino triángulos más
pequeños. Sería “un triángulo de triángulos”.
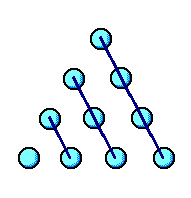
Si no acertaste la conjetura por medio del Álgebra, esta imagen te la
sugerirá con más facilidad. Las bolitas rojas corresponden al cuadrado
de T(4) y las verdes al de T(3). Si no sientes una pequeña emoción al
analizarla es que no te gustan de verdad las Matemáticas.
El fósil de un número
Hoy le damos vueltas a un problema leído en
el blog
http://problemate.blogspot.com/
El fósil de un número
(Fase provincial de Alicante de
la XIX Olimpiada Matemática, 2008)
Dado
un número natural N, se multiplican todas sus cifras. Se repite el
proceso con el resultado obtenido, hasta obtener un número de una cifra
únicamente; a ese número se le llama el fósil de N. Por ejemplo, el
fósil de 327 es 8. Hallar el mayor número natural, con todas sus cifras
distintas, cuyo fósil sea impar.
La solución la puedes leer en
http://solumate.blogspot.com/2008/09/el-fsil-de-un-nmero.html,
y nosotros le
daremos unas vueltas a la idea de “fósil” de un número.
(1)
¿Tienen fósil todos los números naturales?
Te lo puedes
plantar en dos pasos:
(a) El
algoritmo de multiplicar todas las cifras produce una sucesión
estrictamente decreciente y llega a términos de una cifra.
(b) Sólo los
números de una cifra son invariantes en el proceso.
(2)
Construye un algoritmo de hoja de
cálculo tal que dado un número natural,
encuentre su fósil. Puedes restringirlo sólo a números de tres o cuatro
cifras, pero ten en cuenta que si disminuye el número de cifras no
pueden aparecer ceros, que arruinarían el cálculo. En el algoritmo de
la imagen, cuando disminuye el número de cifras aparece la unidad, para
no desvirtuar el producto.
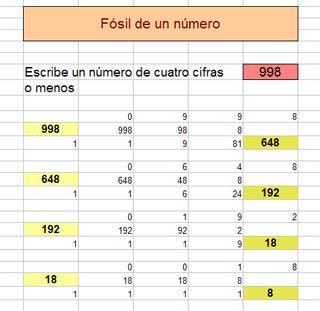
(3)
¿Obtendríamos otro tipo de fósil si sumáramos las cifras en lugar de
multiplicarlas?
(4) Se
pueden aplicar estas ideas al aula si se restringe el estudio a tres
cifras, por ejemplo. Se podrían formar grupos e
intentar que cada uno, con calculadora u hoja de cálculo lograra todos
los fósiles posibles entre 0 y 9, y después se discutieran algunos
casos:
¿Cuándo el
fósil resulta ser cero? ¿Qué crees que hay más, fósiles pares o
impares? ¿Por qué siempre se desemboca en una cifra? Etc.
 Iniciamos la metodología de
"propuestas en ramas" con una colección de propuestas derivadas de un teorema
contenido en el libro “Recreaciones matemáticas 2” de Édouard Lucas:
Iniciamos la metodología de
"propuestas en ramas" con una colección de propuestas derivadas de un teorema
contenido en el libro “Recreaciones matemáticas 2” de Édouard Lucas: