
|
|
 |
|
|
|
|
|
Temas de Estadística
Práctica Antonio Roldán Martínez |
|
|
|
Análisis de la varianza (ANOVA) |
||
|
Estás en Portada > Tema 9 - Análisis de la varianza |
||
| Cuestión - Ejemplo |
Creo que vamos a peor... |
Se han aplicado cuatro métodos distintos para el aprendizaje del concepto de número primo a cuatro grupos de alumnos y alumnas elegidos aleatoriamente. Posteriormente se les ha pasado la misma prueba para valorar la adquisición del concepto, con los siguientes resultados:
| Método A | Método B | Método C | Método D |
| 8 | 16 | 16 | 11 |
| 12 | 12 | 15 | 9 |
| 11 | 13 | 13 | 8 |
| 15 | 15 | 17 | 8 |
| 7 | 19 | 13 | 9 |
| 9 | 16 | 9 | 12 |
| 10 | 13 | 19 | 10 |
| 11 | 10 | 16 | 9 |
| 17 | 6 | 14 | 5 |
| 12 | 11 | 13 | 10 |
Se supone población normal y que las muestras son independientes entre sí. ¿Hay alguna evidencia, al 95% de Nivel de Confianza, de que exista un efecto en la aplicación de los distintos métodos?
Aunque se haya expresado con otras palabras, lo que interesa en esta situación es averiguar si las medias de las cuatro poblaciones representadas por la aplicación de los métodos se pueden considerar iguales o no, es decir:
H0: m1 = m2 = m3 = m4
Lo sorprendente de la técnica que vas a aprender es que para averiguar esto se acude a analizar la varianza. La razón es que si las medias son iguales, la varianza total disminuye, pero si son muy diferentes, aumenta. Es una idea intuitiva que podemos expresar con estas imágenes:

En esta situación, los cuatro grupos están muy cercanos. Su varianza total no será grande. Cada grupo tiene su propia varianza interna.
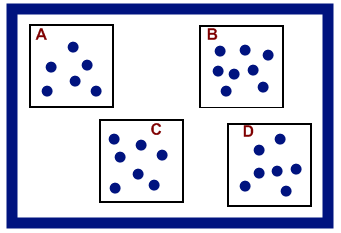
En esta otra, al separarse los grupos, la varianza total aumentará, porque hay más dispersión, pero la varianza interna de cada grupo es la misma. Lo que ha aumentado es la variabilidad Intergrupos
Observando las imágenes puedes entender que si la varianza total aumenta, esto puede deberse a dos causas, o a que haya aumentado la varianza interna de cada grupo, o, lo que es más probable, que se hayan separado las medias y eso ha aumentado la varianza total.
|
Cuando las medias de varios grupos relacionados se separan entre sí, aumenta la varianza total. |
El Análisis de la varianza (ANOVA) nos permite aceptar o rechazar la hipótesis nula H0: m1 = m2 = m3 = m4 descomponiendo la varianza total en dos sumandos: Intragrupos e Intergrupos. Según sean estas cantidades se tomará una decisión u otra.
 |
En el resumen teórico puedes aprender las técnicas del ANOVA |
En la práctica se forman tres sumas de cuadrados distintas y después se restan adecuadamente. Para entenderlo mejor, abre la hoja de cálculo anova.ods y vuelca en ella los datos de la cuestión que estamos estudiando. Lo puedes conseguir con Copiar y Pegar.
S1: Consiste en sumar todos los cuadrados de los datos. En la hoja anova.ods figura a la derecha, y su valor es en este ejemplo 6207.
S2: Se suman los cuadrados de las sumas de los distintos niveles dividido cada uno entre el número de datos. En el ejemplo su valor es de 5901,1
S3: Se obtiene dividiendo el cuadrado de la suma total de todos los niveles dividido entre el número total de datos. En este caso vale 5736,03
Una vez obtenidas estas sumas, se van restando y resultarán las sumas de cuadrados Intergrupos, Intragrupos y Total:
Suma de cuadrados INTRA: S1-S2 = 6207 - 5901,1 = 305,9
Es la suma de cuadrados que corresponde al interior de los niveles, sin tener en cuenta sus diferencia de medias. Sus grados de libertad se obtienen restando el número total (40) menos el número de niveles (4), es decir, 36. Su cociente es el mejor estimador de la varianza de la población, en este caso 8,5
Suma de cuadrados TOTAL: S1-S3 = 6207 - 5736,03 = 470,98
Es la suma total de cuadrados. Sus grados de libertad son N-1, que en este caso son 39, con lo que la varianza total será 470,98/39 = 12,08
Suma de cuadrados INTER: S2-S3 = 5901,1 - 5736,03 = 165,08
Esta suma refleja los desniveles en las medias. Si es alta, puede indicar que las diferencias entre medias son significativas. Sus grados de libertad equivalen al número de niveles menos 1, en el ejemplo 3. La varianza INTER será entonces igual a 55,03
Contraste
El punto importante del ANOVA es el contraste entre unas varianzas y otras, que se realiza, como vimos en el tema anterior, mediante la prueba F.
Observa en el archivo anova.ods cómo se contrasta la igualdad entre las varianzas INTER e INTRA mediante la prueba F. Al dividir nos resulta un valor de F=6,48, muy grande, con un p-valor de 0,001 que la convierte en significativa, luego las medias de los distintos niveles no se pueden considerar iguales.
Como resultado del ANOVA podremos afirmar que en nuestro ejemplo el método de enseñanza ha influido en los resultados.
La tienes contenida en el archivo practica9.pdf
Se está estudiando el tiempo de cocción de un alimento antes de lanzarlo al mercado. Se han formado cuatro grupos y se les ha pedido que midan el tiempo transcurrido hasta que, según su juicio, el alimento quede a punto. Como esta sensación es subjetiva, se usa un ANOVA para estimar la varianza que presenta el experimento. Todos los grupos usan fuentes de calor y utensilios similares. Si la tabla siguiente recoge los resultados redondeados en minutos, ¿qué estimación podríamos hacer de la varianza de la población de estos alimentos? ¿Se observan diferencias entre los grupos?
| Grupo A | Grupo B | Grupo C | Grupo D |
| 7 | 11 | 11 | 9 |
| 7 | 11 | 11 | 9 |
| 8 | 13 | 11 | 10 |
| 7 | 7 | 12 | 9 |
| 9 | 9 | 11 | 10 |
| 8 | 9 | 12 | 8 |
| 11 | 9 | 10 | 10 |
| 12 | 10 | 10 | 10 |
| 9 | 10 | 11 | 12 |
| 10 | 9 | 11 | 9 |
| 10 | 9 | 9 | 9 |
Usa la hoja 1 del archivo anova.ods. Obtendrás que las medias de los grupos son 8,91 9,73 10,82 y 9,55, algo dispersas, y como la F tiene un p-valor de 0,016, se puede catalogar de significativa su diferencia al 5%, luego podemos afirmar que existen diferencias entre los grupos. Quizás haya influido algún otro factor, como la presión atmosférica o los gustos personales. La estimación de la varianza de la población es de 1,79, y su desviación típica de 1,34, algo alta para un experimento que podía haber sido más preciso.
¿Se puede afirmar que la siguiente tabla de doble entrada contiene una interacción significativa entre sus dos factores?
| Nivel 1 | Nivel 2 | |
| Nivel A | 1 2 1 2 3 4 3 4 5 | 2 4 3 4 5 4 3 2 3 1 |
| Nivel B | 3 5 6 5 4 5 3 4 6 | 4 7 6 7 8 7 6 6 5 4 |
| Nivel C | 4 6 5 7 8 9 6 8 6 | 6 8 9 9 8 7 6 7 8 9 |
Vuelca estos datos en el modelo de ANOVA para dos factores y obtendrás estos resultados:
| Fuente variación | SC | G.L. | CM | F | |
| Factor A | 13,38 | 1 | 13,38 | 7,84 | |
| Factor B | 169,3 | 2 | 84,65 | 49,62 | |
| Interacción AB | 3,2 | 2 | 1,6 | 0,94 | |
| Error | 87 | 51 | 1,71 | ||
| TOTAL | 272,88 | 56 |
|
||
La interacción presenta una F cuyo p-valor es 0,398, claramente no significativo.
Para estudiar el efecto del cansancio en una tarea rutinaria, se han contado el número de realizaciones de varios operarios a lo largo del día, con estos resultados:
| En el inicio del trabajo | 12 12 13 14 11 15 9 9 8 10 11 11 10 9 8 10 10 |
| A las cuatro horas | 9 9 9 10 9 7 6 6 9 12 11 10 8 6 9 6 7 |
| A las siete horas | 9 6 7 6 6 7 7 8 8 7 9 9 6 5 6 6 7 9 8 |
¿Se puede afirmar que el tiempo de trabajo transcurrido influye en el rendimiento?
Usa el modelo de un factor. Analiza los resultados:
| Fuente variación | SC | G.L. | CM | F | |
| INTER | 115 | 2 | 57,5 | 19,67 | |
| INTRA | 146,17 | 50 | 2,92 | ||
| TOTAL | 261,17 | 52 | 5,02 | ||
La F=19,67 es claramente significativa. Sí existe una influencia del cansancio.
Análisis de la regresión
Las técnicas del Análisis de la varianza se pueden aplicar también al estudio de la regresión lineal entre dos variables. Basta considerar los valores de X como niveles de un factor y sustituir las sumas INTER e INTRA por sus equivalentes REGRESIÓN y ERROR.
Consulta el resumen teórico, en el que sólo está esbozada la teoría, o completa con cualquier manual de tipo medio.
Para que comprendas mejor la teoría desarrollaremos un ejemplo:
En tiempos de crisis se ha efectuado un estudio sobre el nivel de gasto de unas familias. Se han comparado cuatro niveles de ingreso familiar con el gasto mensual para intentar descubrir una relación lineal entre ambos. Los resultados, en miles de euros, han sido los siguientes:
| Nivel en miles de euros | Gastos |
| 1,5 | 1 1,2 0,9 1,4 1,5 1,3 1,2 1,1 1,4 1,3 |
| 2 | 1,5 1,5 1,9 2 1,8 1,7 1,5 1,3 |
| 2,5 | 2,4 2,5 2 1,7 2 1,8 1,9 1,8 2 2,4 2,5 |
| 3 | 2,4 2,3 2,6 3 2,8 2,7 2,8 2,6 3 |
¿Es significativa la relación lineal entre ambos? Expresado de otra forma, ¿Es la pendiente significativamente distinta de 0?
Volcamos estos datos en la tercera hoja (Regresión) del archivo anova.ods.
En las celdas L18 y L19 podemos leer los coeficientes de la ecuación de regresión Y' = 0,95789X - 0,24211. Podemos interpretar que cada incremento de un euro en el ingreso se traduce en un incremento de 0,95 en el gasto. Como de hecho se ha ahorrado más, querrá decir que hay una base fija del mismo (representada por -0,24), y que aumentos de ingreso no se traducen en incrementos proporcionales en el gasto, sino que hay una base fija que se dedica al ahorro.
Pero, ¿es significativo?
En el análisis de ANOVA vemos lo siguiente:
| Fuente variación | SC | G.L. | CM | F |
| Regresión | 10,9 | 1 | 10,9 | 179,33 |
| Error | 2,19 | 36 | 0,06 | |
| TOTAL | 13,08 | 37 | 0,35 |
|
|
|
|
|
|
|
P-valor de F | 0,000 |
|
|
|
|
|
|
|
|
Fcrítica al 90% | 2,85 | Significativa |
|
|
Fcrítica al 95% | 4,11 | Significativa |
|
|
Fcrítica al 99% | 7,4 | Significativa |
|
|
|
|
|
Casi toda la suma de cuadrados (13,08) es explicada por la regresión (10,9), por lo que F es claramente significativa a todos los niveles usuales. El error estimado es muy pequeño (0,06), lo que indica que la población es bastante homogénea.
Podemos, pues, afirmar que existe una relación lineal con pendiente significativamente distinta de cero, lo que traducido a lenguaje llano significa que sí existe influencia lineal de los ingresos en los gastos.
En este archivo dispones de tres hojas para el estudio de ANOVA: Para un factor, de dos factores y para la regresión. Puedes limitarte a rellenar los datos y después interpretar los resultados.
Esta herramienta pertenece al tema 5, pero contiene una hoja con el análisis de la regresión, y te puede valer para repasar lo que hayas aprendido en este tema 9.